
【题目】如图,在矩形ABCD中,∠ADC的平分线与AB交于E,点F在DE的延长线上,∠BFE=90°,连接AF、CF,CF与AB交于G.有以下结论:
①AE=BC
②AF=CF
③BF2=FGFC
④EGAE=BGAB
其中正确的个数是( )

A. 1 B. 2 C. 3 D. 4
【答案】C
【解析】
①只要证明△ADE为等腰直角三角形即可
②只要证明△AEF≌△CBF(SAS)即可;
③假设BF2=FGFC,则△FBG∽△FCB,推出∠FBG=∠FCB=45°,由∠ACF=45°,推出∠ACB=90°,显然不可能,故③错误,
④由△ADF∽△GBF,可得![]() ,由EG∥CD,推出
,由EG∥CD,推出![]() ,推出
,推出![]() ,由AD=AE,EGAE=BGAB,故④正确,
,由AD=AE,EGAE=BGAB,故④正确,
①DE平分∠ADC,∠ADC为直角,
∴∠ADE=![]() ×90°=45°,
×90°=45°,
∴△ADE为等腰直角三角形,
∴AD=AE,
又∵四边形ABCD矩形,
∴AD=BC,
∴AE=BC
②∵∠BFE=90°,∠BFE=∠AED=45°,
∴△BFE为等腰直角三角形,
∴则有EF=BF
又∵∠AEF=∠DFB+∠ABF=135°,∠CBF=∠ABC+∠ABF=135°,
∴∠AEF=∠CBF
在△AEF和△CBF中,AE=BC,∠AEF=∠CBF,EF=BF,
∴△AEF≌△CBF(SAS)
∴AF=CF
③假设BF2=FGFC,则△FBG∽△FCB,
∴∠FBG=∠FCB=45°,
∵∠ACF=45°,
∴∠ACB=90°,显然不可能,故③错误,
④∵∠BGF=180°-∠CGB,∠DAF=90°+∠EAF=90°+(90°-∠AGF)=180°-∠AGF,∠AGF=∠BGC,
∴∠DAF=∠BGF,∵∠ADF=∠FBG=45°,
∴△ADF∽△GBF,
∴![]() ,
,
∵EG∥CD,
∴![]() ,
,
∴![]() ,∵AD=AE,
,∵AD=AE,
∴EGAE=BGAB,故④正确,
故选C.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知∠AOB=30°,P是OA上的一点,OP=24cm,以r为半径作⊙P.

(1)若r=12cm,试判断⊙P与OB位置关系;
(2)若⊙P与OB相离,试求出r需满足的条件.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:有一个直角三角形ABC,∠C=90°,AC=10,BC=5,一条线段PQ=AB,P、Q两点分别在AC和过点A且垂直于AC的射线AX上运动,问P点运动到离A的距离等于___________时,ΔABC和ΔPQA全等.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
问题情境:在数学活动课上,老师出示了这样一个问题:如图1,在矩形ABCD中,AD=2AB,E是AB延长线上一点,且BE=AB,连接DE,交BC于点M,以DE为一边在DE的左下方作正方形DEFG,连接AM.试判断线段AM与DE的位置关系.
探究展示:勤奋小组发现,AM垂直平分DE,并展示了如下的证明方法:
证明:∵BE=AB,∴AE=2AB.
∵AD=2AB,∴AD=AE.
∵四边形ABCD是矩形,∴AD∥BC.
∴![]() .(依据1)
.(依据1)
∵BE=AB,∴![]() .∴EM=DM.
.∴EM=DM.
即AM是△ADE的DE边上的中线,
又∵AD=AE,∴AM⊥DE.(依据2)
∴AM垂直平分DE.
反思交流:
(1)①上述证明过程中的“依据1”“依据2”分别是指什么?
②试判断图1中的点A是否在线段GF的垂直平分线上,请直接回答,不必证明;
(2)创新小组受到勤奋小组的启发,继续进行探究,如图2,连接CE,以CE为一边在CE的左下方作正方形CEFG,发现点G在线段BC的垂直平分线上,请你给出证明;
探索发现:
(3)如图3,连接CE,以CE为一边在CE的右上方作正方形CEFG,可以发现点C,点B都在线段AE的垂直平分线上,除此之外,请观察矩形ABCD和正方形CEFG的顶点与边,你还能发现哪个顶点在哪条边的垂直平分线上,请写出一个你发现的结论,并加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为2的正△ABC的边BC在直线l上,两条距离为l的平行直线a和b垂直于直线l,a和b同时向右移动(a的起始位置在B点),速度均为每秒1个单位,运动时间为t(秒),直到b到达C点停止,在a和b向右移动的过程中,记△ABC夹在a和b之间的部分的面积为s,则s关于t的函数图象大致为( )

A.  B.
B.  C.
C. 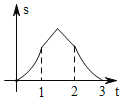 D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,若△ABC内一点P满足∠PAC=∠PCB=∠PBA,则称点P为△ABC的布罗卡尔点,三角形的布罗卡尔点是法国数学家和数学教育家克雷尔首次发现,后来被数学爱好者法国军官布罗卡尔重新发现,并用他的名字命名,布罗卡尔点的再次发现,引发了研究“三角形几何”的热潮.已知△ABC中,CA=CB,∠ACB=120°,P为△ABC的布罗卡尔点,若PA=![]() ,则PB+PC=_____.
,则PB+PC=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形ABCD在平面直角坐标系中,点A(1,8),B(1,6),C(7,6),点X,Y分别在x,y轴上.
(1)请直接写出D点的坐标 ;
(2)连接OB、OD,OD交BC于点E,∠BOY的平分线和∠BEO的平分线交于点F,若∠BOE=n,求∠OFE的度数.
(3)若长方形ABCD以每秒![]() 个单位的速度向下运动,设运动时间为t秒,问在第一象限内是否存在某一时刻t,使△OBD的面积等于长方形ABCD的面积的
个单位的速度向下运动,设运动时间为t秒,问在第一象限内是否存在某一时刻t,使△OBD的面积等于长方形ABCD的面积的![]() ?若存在,请求出t的值,若不存在,请说明理由。
?若存在,请求出t的值,若不存在,请说明理由。


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC、∠ACB的角平分线交于点O,MN过点O,且MN∥BC,分别交AB、AC于点M、N.若BM=3cm,CN=2cm,则MN=_____cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】D为等边△ABC的边AC上一点,E为直线AB上一点,CD=BE.
(1)如图1,求证:AD=DE;
(2)如图2,DE交CB于点F.
①若DE⊥AC,CF=6,求BF的长;
②求证:DF=EF.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com