
【题目】D为等边△ABC的边AC上一点,E为直线AB上一点,CD=BE.
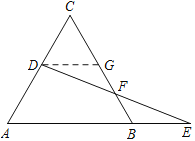
(1)如图1,求证:AD=DE;
(2)如图2,DE交CB于点F.
①若DE⊥AC,CF=6,求BF的长;
②求证:DF=EF.

【答案】(1)证明见解析;(2)①3;②证明见解析
【解析】
(1)根据等边三角形的性质可得AB=AC,∠A=60°,由CD=BE,利用线段的和差关系可得AD=AE,即可证明△ADE是等边三角形,可得AD=DE;(2)①由DE⊥AC可得∠CFD=30°,根据含30°角的直角三角形的性质可求出CD的长,可得BE的长,根据∠BFE=∠CFD=30°,∠E=30°,可得BF=BE,即可得答案;②过点D作DG∥AB,交CB于点G,可得∠CGD=∠ABC=60°,∠GDF=∠E,由∠C=60°可证明△CDG是等边三角形,可得CD=DG,进而可得DG=BE,利用AAS可证明△GDF≌△BEF,即可得DF=EF.
(1)∵△ABC是等边三角形,
∴AB=AC,∠A=60°,
∵CD=BE,
∴AC=CD=AB-BE,即AD=AE,
∴△ADE是等边三角形,
∴AD=DE;
(2)①∵DF⊥AC,
∴∠CDF=90°,
∵∠C=60°,
在Rt△CDF中,∠CFD=30°,
∴CD=![]() CF=
CF=![]() ×6=3,
×6=3,
∵CD=BE,
∴BE=3,
∵∠BFE=∠CFD=30°,∠E=30°,
∴BE=BF,
∴BF=3;
②如图,过点D作DG∥AB,交CB于点G,
∴∠CGD=∠ABC=60°,∠GDF=∠E,
∵∠C=60°,
∴△CDG是等边三角形,
∴CD=DG,
∵CD=BE,
∴DG=BE,
在△GDF和△BEF中, ,
,
∴△GDF≌△BEF(AAS),
∴DF=EF.


科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,∠ADC的平分线与AB交于E,点F在DE的延长线上,∠BFE=90°,连接AF、CF,CF与AB交于G.有以下结论:
①AE=BC
②AF=CF
③BF2=FGFC
④EGAE=BGAB
其中正确的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,为了测量出一垂直水平地面的某高大建筑物AB的高度,一测量人员在该建筑物附近C处,测得建筑物顶端A处的仰角大小为45°,随后沿直线BC向前走了100米后到达D处,在D处测得A处的仰角大小为30°,求建筑物AB的高度.(注:结果保留到0.1,![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在下列条件中,不能证明△ABD≌△ACD的是( ).

A.BD=DC, AB=AC B.∠ADB=∠ADC,BD=DC
C.∠B=∠C,∠BAD=∠CAD D. ∠B=∠C,BD=DC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】20、如图,直角坐标系中,△ABC的顶点都在网格点上,其中,C点坐标为(1,2).

(1)填空:点A关于X轴对称的点的坐标是 ___,点B关于Y轴对称的点的坐标是 ;
(2)将△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到△A′B′C′.请写出△A′B′C′的三个顶点坐标;
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB//CD.

(1)如图①,若∠ABE=40o,∠BEC=140o,∠ECD=_________o
(2)如图①,试探究∠ABE,∠BEC,∠ECD的关系,并说明理由;
(3)如图②,若CF平分∠ECD,且满足CF∥BE,试探究∠ECD,∠ABE的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
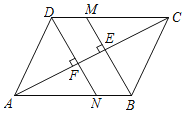
【题目】如图,在ABCD中,过B点作BM⊥AC于点E,交CD于点M,过D点作DN⊥AC于点F,交AB于点N.
(1)求证:四边形BMDN是平行四边形;
(2)已知AF=12,EM=5,求AN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】最近雾霾天气频繁,使得空气净化器得以畅销.某商场代理销售某种空气净化器,其进价是500元/台,经过市场销售后发现,当售价是1000元/台时,每月可售出50台,且售价每降低20元,每月就可多售出5台.若供货商规定这种空气净化器售价不能低于600元/台,代理销售商每月要完成不低于60台的销售任务.
(1)试确定月销售量y(台)与售价x(元/台)之间的函数关系式,并求出自变量x的取值范围.
(2)当售价x(元/台)定为多少时,商场每月销售这种空气净化器所获得的利润w(元)最大?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com