
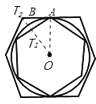
【题目】如图,有一个圆O和两个正六边形T1,T2. T1的6个顶点都在圆周上,T2的6条边都和圆O相切(我们称T1,T2分别为圆O的内接正六边形和外切正六边形).

(1)设T1,T2的边长分别为a,b,圆O的半径为r,求r:a及r:b的值;
(2)求正六边形T1,T2的面积比S1:S2的值.
【答案】(1)![]() :2(2)3:4
:2(2)3:4
【解析】
根据题意画出图形,连接OE、OG,OF,由正六边形T1,得到∠EOF为60°,从而得到△EOF为等边三角形,即a=r,故得到a:r=1:1;在Rt△EOG中,由OG为角平分线,得到∠EOG=30°,利用特殊角的三角函数可求出OE及OG的长,即为r:b的比值,然后求出a:b的比值,根据正六边形T1,T2相似,其面积之比等于边长之比的平方,即可求出面积之比.
(1)连接圆心O和T1的6个顶点可得6个全等的正三角形.
所以r:a=1:1;
连接圆心O和T2相邻的两个顶点,得以圆O半径为高的正三角形,
所以r:b=AO:BO=sin60°=![]() :2;
:2;
(2)T1:T2的边长比是![]() :2,所以S1:S2=(a:b)2=3:4.
:2,所以S1:S2=(a:b)2=3:4.


科目:初中数学 来源: 题型:
【题目】先化简再求值:
(1)(x+y)(xy)(4x3y4xy3)÷2xy,其中x=1,y=![]() .
.
(2)实数x满足x22x2=0,求代数式(2x1)2x(x+4)+(x3)(x+3)的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下图是我国北方某地一棵树在一天不同时刻拍下的五张图片,仔细观察后回答下列问题.
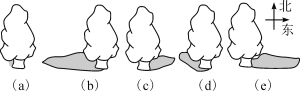
(1)说出这五张图片所对应的时间的先后顺序;
(2)根据生活经验,谈谈由早到晚该地物体影子的长短变化规律.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】兴趣小组的同学要测量树的高度.在阳光下,一名同学测得一根长为1米的竹竿的影长为0.4米,同时另一名同学测量树的高度时,发现树的影子不全落在地面上,有一部分落在教学楼的第一级台阶上,测得此影长为0.2米,一级台阶高为0.3米,如图所示,若此时落在地面上的影长为4.4米,求树的高度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小王、小李在班里选拔赛中并列第一名,小王提议通过摸球的方式来决定谁代表班级参加学校数学竞赛,规则如下:
在两个盒子内分别装入标有数字1,2,3,4的四个标有数字1,2,3的三个完全相同的小球,分别从两个盒子中各摸出一个球,如果所摸出的球上的数字之和小于5,那么小王去参加,否则就是小李去参加.
(1)用树状图或列表法求出小王去参加的概率;
(2)小李说:“可以,这种规则公平”,你认同他的说法吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某幼儿园计划购进一批甲、乙两种玩具,已知一件甲种玩具的价格与一件乙种玩具的价格的和为40元,用90元购进甲种玩具的件数与用150元购进乙种玩具的件数相同.
(1)求每件甲种、乙种玩具的价格分别是多少元?
(2)该幼儿园计划用3500元购买甲、乙两种玩具,由于采购人员把甲、乙两种玩具的件数互换了,结果需4500元,求该幼儿园原计划购进甲、乙两种玩具各多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知M(x,y)是平面直角坐标系xOy中的点,其中x是从l、2、3三个数中任取的一个数,y是从l、2、3、4四个数中任取的一个数 .
(l)计算由x、y确定的点M(x,y)在函数y= -x+5的图象上的概率;
(2)小明和小红约定做一个游戏,其规则为:若x、y满足xy>6则小明胜;若x、y满足xy<6则小红胜,这个游戏公平吗?说明理由. 若不公平,请写出公平的游戏规则;
(3)定义“点M(x,y)在直线x+y=n上”为事件A(2≤n≤7,n为整数),则当A的概率最大时,n的所有可能的值为 .(不需要解答过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,∠B=30°,AB=AC,O是两条对角线的交点,过点O作AC的垂线分别交边AD,BC于点E,F,点M是边AB的一个三等分点.连接MF,则△AOE与△BMF的面积比为________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com