
| 2014 |
| x |
| 1 |
| 2 |
| 2014 |
| x |
|
|
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2014 |
| x |
| 2014 |
| x |
| 2014 |
| x |
|
|
|
|
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
|
|
|


科目:初中数学 来源: 题型:
 如图,⊙O的半径OA,OB,且OA⊥OB,连结AB.现在⊙O上找一点C,使OA2+AB2=BC2,则∠OAC的度数为( )
如图,⊙O的半径OA,OB,且OA⊥OB,连结AB.现在⊙O上找一点C,使OA2+AB2=BC2,则∠OAC的度数为( )| A、15°或75° |
| B、20°或70° |
| C、20° |
| D、30° |
查看答案和解析>>
科目:初中数学 来源: 题型:
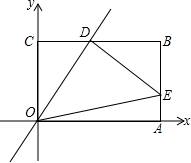 如图,在平面直角坐标系中,矩形OABC的顶点A在x轴上,点C在y轴上,点B的坐标是(8,6),正比例函数y=kx的图象交BC于点D,DE⊥OD,交AB于点E,连结OE.
如图,在平面直角坐标系中,矩形OABC的顶点A在x轴上,点C在y轴上,点B的坐标是(8,6),正比例函数y=kx的图象交BC于点D,DE⊥OD,交AB于点E,连结OE.查看答案和解析>>
科目:初中数学 来源: 题型:
 已知:如图,在平面直角坐标系xOy中,点A(2
已知:如图,在平面直角坐标系xOy中,点A(2| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
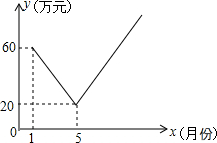 保护生态环境,实行“节能减排”的理念已深入人心.我市某工厂从2014年1月开始,进行机器设备更新,产业转型换代的改造,改造期间利润明显下降,从1月份利润60万元逐月等额下降,到5月份利润为20万元;5月底改造完成,从这时起,该厂每个月的利润都比上个月增加15万元.设第x个月的利润为y(万元),函数图象如图.
保护生态环境,实行“节能减排”的理念已深入人心.我市某工厂从2014年1月开始,进行机器设备更新,产业转型换代的改造,改造期间利润明显下降,从1月份利润60万元逐月等额下降,到5月份利润为20万元;5月底改造完成,从这时起,该厂每个月的利润都比上个月增加15万元.设第x个月的利润为y(万元),函数图象如图.查看答案和解析>>
科目:初中数学 来源: 题型:
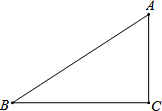 如图,在直角三角形ABC中,∠ACB=90°.
如图,在直角三角形ABC中,∠ACB=90°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com