
【题目】初三年(4)班要举行一场毕业联欢会,主持人同时转动下图中的两个转盘,由一名同学在转动前来判断两个转盘上指针所指的两个数字之和是奇数还是偶数,如果判断错误,他就要为大家表演一个节目;如果判断正确,他可以指派别人替自己表演节目.现在轮到小明来选择,小明不想自己表演,于是他选择了偶数.小明的选择合理吗?从概率的角度进行分析(要求用树状图或列表方法求解)

【答案】不合理。理由见解析.
【解析】依据题意先用列表法或画树状图法分析所有等可能的出现结果,然后根据概率公式分别求出两个数字之和是奇数与是偶数的概率,根据概率的大小即可判断小明的选择是否合理.
解:小明的选择不合理;
列表得
2 | 3 | 4 | 6 | |
3 | 5 | 6 | 7 | 9 |
5 | 7 | 8 | 9 | 11 |
8 | 10 | 11 | 12 | 14 |
∴共出现12中等可能的结果,
其中出现奇数的次数是7次,概率为![]() ,
,
出现偶数的次数为5次,概率为![]() ,
,
∵![]() ,即出现奇数的概率较大,
,即出现奇数的概率较大,
∴小明的选择不合理.
“点睛”本题考查的是用列表法或画树状图法求概率.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件.注意哪个概率大,选择哪个的可能性就大.用到的知识点为:概率=所求情况数与总情况数之比.


科目:初中数学 来源: 题型:
【题目】最近几年,某市持续大面积雾霾天气让环保和健康问题成为焦点,为了调查学生对雾霾天气知识的了解程度,某校在全校学生中抽取400名同学做了一次调查,调查结果共分为四个等组A.非常了解;B.比较了解;C.基本了解;D.不了解
根据调查统计结果,绘制了不完整的三种统计图表.
对雾霾天气了解程度的 条形统计图 | 对雾霾天气了解程度的 扇形统计图 | 对雾霾天气了解程度的 统计表 | |
图1 |
图2 | 对雾霾的了解程度 | 百分比 |
A.非常了解 | 5% | ||
B.比较了解 | m | ||
C.基本了解 | 45% | ||
D.不了解 | n | ||
请结合统计图表,回答下列问题:
(1)本次参与调查的学生选择“A.非常了解”的人数为__________人,m=__________,n=__________;
(2)请在图1中补全条形统计图;
(3)请计算在图2所示的扇形统计图中,D部分扇形所对应的圆心角是多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】遵义市某中学为了搞好“创建全国文明城市”的宣传活动,对本校部分学生(随机抽查)进行了一次相关知识了解程度的调查测试(成绩分为A、B、C、D、E五个组,x表示测试成绩).通过对测试成绩的分析,得到如图所示的两幅不完整的统计图.请你根据图中提供的信息解答以下问题:

(1)参加调查测试的学生为多少人?
(2)将条形统计图补充完整;
(3)本次调查测试成绩中的中位数落在哪组内?
(4)若测试成绩在80分以上(含80分)为优秀,该中学共有学生2600人,请你根据样本数据估计全校学生测试成绩为优秀的总人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形OABC为矩形,A点在x轴上,C点在y轴上,矩形一角经过翻折后,顶点B落在OA边的点G处,折痕为EF,F点的坐标是(4,1),∠FGA=30°.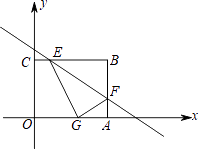
(1)求B点坐标.
(2)求直线EF解析式.
(3)若点M在y轴上,直线EF上是否存在点N,使以M、N、F、G为顶点的四边形是平行四边形?若存在,求N点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线经过点A(4,0),B(0,4),C(6,6).
(1)求抛物线的表达式;
(2)证明:四边形AOBC的两条对角线互相垂直;
(3)在四边形AOBC的内部能否截出面积最大的DEFG?(顶点D,E,F,G分别在线段AO,OB,BC,CA上,且不与四边形AOBC的顶点重合)若能,求出DEFG的最大面积,并求出此时点D的坐标;若不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,AB是⊙O的直径,点C为⊙O上一点,OF⊥BC于点F,交⊙O于点E,AE与BC交于点H,点D为OE的延长线上一点,且∠ODB=∠AEC.
(1)求证:BD是⊙O的切线;
(2)求证:CE2=EHEA;
(3)若⊙O的直径为5,sinA=![]() ,求BH的长.
,求BH的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com