Question

【题目】已知，如图，AB是⊙O的直径，点C为⊙O上一点，OF⊥BC于点F，交⊙O于点E，AE与BC交于点H，点D为OE的延长线上一点，且∠ODB=∠AEC．

（1）求证：BD是⊙O的切线；

（2）求证：CE2=EHEA；

（3）若⊙O的直径为5，sinA=，求BH的长．

Answer 1

【答案】（1）证明见试题解析；（2）证明见试题解析；（3）．

【解析】试题分析：（1）由圆周角定理和已知条件证出∠ODB=∠ABC，再证出∠ABC+∠DBF=90°，即∠OBD=90°，即可得出BD是⊙O的切线；

（2）连接AC，由垂径定理得出，得出∠CAE=∠ECB，再由公共角∠CEA=∠HEC，证明△CEH∽△AEC，得出对应边成比例，即可得出结论；

（3）连接BE，由圆周角定理得出∠AEB=90°，由三角函数求出BE，再根据勾股定理求出EA，得出BE=CE=6，由（2）的结论求出EH，然后根据勾股定理求出BH即可．

试题解析：（1）∵∠ODB=∠AEC，∠AEC=∠ABC，∴∠ODB=∠ABC，

∵OF⊥BC，∴∠BFD=90°，∴∠ODB+∠DBF=90°，∴∠ABC+∠DBF=90°，

即∠OBD=90°，∴BD⊥OB，∴BD是⊙O的切线；

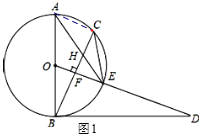
（2）连接AC，如图1所示：

∵OF⊥BC，∴， ∴∠CAE=∠ECB，

∵∠CEA=∠HEC，∴△CEH∽△AEC，∴，∴CE2=EHEA；

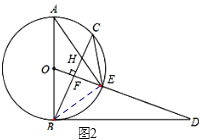
（3）连接BE，如图2所示：

∵AB是⊙O的直径，∴∠AEB=90°，

∵⊙O的半径为，sin∠BAE=，∴AB=5，BE=ABsin∠BAE=5×=3，∴EA==4，

∵，∴BE=CE=3，∵CE2=EHEA，∴EH=

∴在Rt△ BEH中，BH==．