练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    19．已知一次函数y=2x-4与y=-x+2．
    （1）在同一坐标系中画出它们的图象；并写出它们的图象的交点坐标．
    （2）求它们和y轴所围图形的面积．

    分析 （1）根据描点法，可得函数图象；
    （2）根据三角形的面积公式，可得答案．

    解答 解：（1）如图，
    交点A（2，0），
    （2）它们和y轴所围图形的面积SABC=$\frac{1}{2}$BC•OA=$\frac{1}{2}$×6×2=6．

    点评 本题考查了一次函数图象，利用描点法画一次函数图象，又利用了三角形的面积公式．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    9．计算
    （1）$\sqrt{\frac{1}{7}}$$+\sqrt{63}$$-\sqrt{700}$
    （2）$\sqrt{\frac{1}{3}}$×$\sqrt{108}$$-\frac{\sqrt{8}×\sqrt{2}}{\sqrt{4}}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

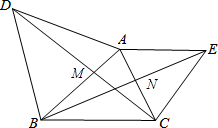    10．如图，△ABD、△AEC都是等边三角形．AB、CD相交于M，AC、BE相交于N，∠MAN=60°．求证：
    （1）BE=DC；
    （2）AM=AN．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．一次函数的图象与直线y=2x+5在y轴上交于一点A，且过点B（-3，8），求这个函数的解析式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．（1）已知线段AB=8，点C在线段AB的延长线上，M、N分别是线段AC与线段BC的中点，求线段MN的长；
    （2）已知线段AB=8cm，点C在线段AB的反向延长线上，M、N分别是线段AC与线段BC的中点，则线段MN的长为4cm．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    4．Rt△ABC中，CD是斜边AB上的高，那么与sinB的值相等的线段的比是$\frac{AD}{AC}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

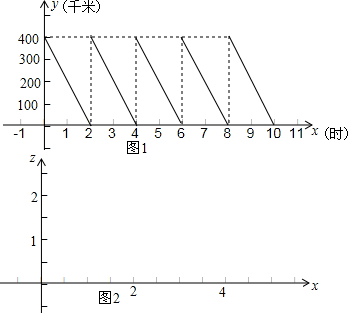    3．我们已经研究过函数的增减性（即单调性）、函数的对称性（即奇偶性）、函数的有界性，今天我们来研究一下函数的周期性．生活中有很多具有周期性的例子，如钟表的指针绕钟表圆心周而复始的旋转等，再如下面的例子：
    甲乙两地开通了动车，设两地相距400千米，动车速度为200千米/时，若每隔2小时就有一辆动车从甲地发出，共有5辆动车，设第1辆动车出发的时刻为0时，第1辆动车出发时间为x小时，若设动车与乙地的距离为y1千米，则上面描述可用下面的函数图象来表示（如图1）
    其实，这五条线段可以用如下的函数解析式来表达：
    y1=-200（x-2i）+400（2i≤x≤2i+2，i=0，1，2，3，4）
    （1）若在第一辆动车出发的同时，有一辆慢车从乙地开往甲地，速度为80千米/时，设慢车与乙地的距离为y2千米，在图1 中画出这辆慢车运行的函数图象，并结合图象说明整个运行过程中，慢车与动车共相遇多少次？
    （2）已知z=（x-1-2i）2（2i≤x≤2i+2，i=0，1，2，3）
    ①在图2的平面直角坐标系中画出这个函数的图象．
    ②当x=2.5和x=5.4时，对应的函数值分别为z1和z2，比较z1和z2的大小．
    （3）若关于x的方程k（x+1）=（x-1-2i）2（2i≤x≤2i+2），i=0，1，2，3）有5个不相等的实数根，求k的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．已知函数y=2x+4，
    （1）求该函数与坐标轴的交点坐标；
    （2）画出该函数的图象；
    （3）点C（2，p）在这条直线上，求p的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    1．如图，若正方形OABC的顶点B和正方形ADEF的顶点E都在函数y=$\frac{1}{x}$（x＞0）的图象上，则点B的坐标为（1，1），点E的坐标为（$\frac{1+\sqrt{5}}{2}$，$\frac{-1+\sqrt{5}}{2}$）．

    查看答案和解析>>

    同步练习册答案