【题目】如图，已知
为直线
上一点，过点向直线上方引三条射线
、
、
，且平分
，
．
（1）若
°，求
的度数；
（2）若
°，求
的度数；
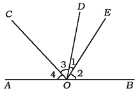
【答案】（1）72°；（2）60°．
【解析】
（1）依据∠1=18°，∠2=3∠1，可得∠2=54°，进而得出∠AOD的度数，再根据OC平分∠AOD，可得∠3=54°，进而得到∠COE的度数；
（2）根据角平分线的定义和平角的定义，借助于图形得到：x°+∠2+2（70°-x°）=180°，则∠2=40°+x°，进而得到40°+x°=3x°，则易求∠2的度数．
解：（1）∵
°，
，
∴
°，
∴
°－
°－18°－54°=108°，
∵OC平分
，
∴
°， ∠COE=∠1＋∠3=18°＋54°=72°
（2）设∠1=
°，
∵OC平分，
∠1＋∠3=70°，
∴∠3=∠4=70°－°，
又∵∠1＋∠2＋∠3＋∠4=180°，
∴°＋∠2＋2（70°－°）=180°，
∴∠2=40°＋°
∵，
∴ 40°＋°=3°，解得=20，
∴=3×20°=60°，即∠2的度数为60°．
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】如图，某兴趣小组用高为1.6米的仪器测量塔CD的高度．由距塔CD一定距离的A处用仪器观察建筑物顶部D的仰角为β，在A和C之间选一点B，由B处用仪器观察建筑物顶部D的仰角为α．测得A，B之间的距离为10米，tanα=1.6，tanβ=1.2，试求塔CD的大约高度．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，纸上有五个边长为1的小正方形组成的图形纸（图1），我们可以把它剪开拼成一个正方形（图2）．
（1）图2中拼成的正方形的面积是 _________ ；边长是 _________ ；（填实数）
（2）请你在图3中画一个面积为5的正方形，要求所画正方形的顶点都在格点上．请用虚线画出．
（3）你能把十个小正方形组成的图形纸（图4），剪开并拼成正方形吗？若能，请仿照图2的形式把它重新拼成一个正方形．并求出它的边长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，下列图案均是长度相同的火柴按一定的规律拼搭而成：第1个图案需7根火柴，第2个图案需13根火柴，…，依此规律，第11个图案需（ ）根火柴．
A. 156 B. 157 C. 158 D. 159
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在学习“用直尺和圆规作一个角等于已知角”时，教科书介绍如图：对于“想一想”中的问题，下列回答正确的是（ ）
A. 根据“边边边”可知，△C′O′D′≌△COD，所以∠A′O′B′=∠AOB
B. 根据“边角边”可知，△C′O′D′≌△COD，所以∠A′O′B′=∠AOB
C. 根据“角边角”可知，△C′O′D′≌△COD，所以∠A′O′B′=∠AOB
D. 根据“角角边”可知，△C′O′D′≌△COD，所以∠A′O′B′=∠AOB
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，O为直线AB上一点，∠COE=90°,OF平分∠AOE.
（1）若∠COF=40°，求∠BOE的度数.
（2）若∠COF=α（0°＜α＜90°），则∠BOE=______（用含α的式子表示）.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，七巧板由图中标号为“
”、“
”、“
”、“
”、“
”、“
”、“
”的七块板组成，七巧板是我们祖先的一项卓越创造，被称为“东方魔板”，它虽然仅有七块板组成，但用它们可以拼出各种各样的图形.请你按下列要求画出所拼的图，图中往上标号：
①用其中的四块板拼成一个三角形；
②用其中的五块板拼成一个正方形.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在数轴上点A表示数a，点C表示数c，且
.我们把数轴上两点之间的距离用表示两点的大写字母一起标记.
比如，点A与点B之间的距离记作AB.
(1)求AC的值；
(2)若数轴上有一动点D满足CD＋AD=36，直接写出D点表示的数；
(3)动点B从数1对应的点开始向右运动，速度为每秒1个单位长度，同时点A，C在数轴上运动，点A、C的速度分别为每秒 3个单位长度，每秒4个单位长度，运动时间为t秒.
①若点A向右运动，点C向左运动，AB=BC，求t的值.
②若点A向左运动，点C向右运动，2AB－m×BC的值不随时间t的变化而改变，请求出m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
