
【题目】如图,七巧板由图中标号为“![]() ”、“
”、“![]() ”、“
”、“![]() ”、“
”、“![]() ”、“
”、“![]() ”、“
”、“![]() ”、“
”、“![]() ”的七块板组成,七巧板是我们祖先的一项卓越创造,被称为“东方魔板”,它虽然仅有七块板组成,但用它们可以拼出各种各样的图形.请你按下列要求画出所拼的图,图中往上标号:
”的七块板组成,七巧板是我们祖先的一项卓越创造,被称为“东方魔板”,它虽然仅有七块板组成,但用它们可以拼出各种各样的图形.请你按下列要求画出所拼的图,图中往上标号:

①用其中的四块板拼成一个三角形;
②用其中的五块板拼成一个正方形.
科目:初中数学 来源: 题型:
【题目】如图,OA=2,以点A为圆心,1为半径画⊙A与OA的延长线交于点C,过点A画OA的垂线,垂线与⊙A的一个交点为B,连接BC

(1)线段BC的长等于 ;
(2)请在图中按下列要求逐一操作,并回答问题:
①以点 为圆心,以线段 的长为半径画弧,与射线BA交于点D,使线段OD的长等于![]() ;
;
②连OD,在OD上画出点P,使OP得长等于![]() ,请写出画法,并说明理由.
,请写出画法,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)计算下列各题:
①2x2﹣4x+1+2x﹣5x2
②(8x﹣3x2)﹣5xy﹣2(3xy﹣2x2)
(2)先化简,再求值:(3x2y+5x)﹣[x2y﹣4(x﹣x2y)],其中(x+2)2+|y﹣3|=0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(概念学习)
规定:求若干个相同的有理数(均不等于0)的除法运算叫做除方,如2÷2÷2,(﹣3)÷(﹣3)÷(﹣3)÷(﹣3)等.类比有理数的乘方,我们把2÷2÷2记作2③,读作“2的圈3次方”,(﹣3)÷(﹣3)÷(﹣3)÷(﹣3)记作(﹣3)④,读作“﹣3的圈4次方”,一般地,把n个a(a≠0)记作a,读作“a的圈n次方”.
(初步探究)
(1)直接写出计算结果:2③= ,(﹣![]() )⑤= ;
)⑤= ;
(深入思考)
我们知道,有理数的减法运算可以转化为加法运算,除法运算可以转化为乘法运算,有理数的除方运算如何转化为乘方运算呢?
(1)试一试:仿照上面的算式,将下列运算结果直接写成乘方的形式.
(﹣3)④= ;5⑥= ;(﹣![]() )⑩= .
)⑩= .
(2)想一想:将一个非零有理数a的圈n次方写成乘方的形式等于 ;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为缓解城市汽车交通拥堵,减少汽车尾气对大气的污染. 某区政府投放了大量公租自行车供市民使用. 到2016年底,全区已有公租自行车2 500辆,摆放点60个. 预计到2018年底,全区将有公租自行车5 000辆,并且平均每个摆放点的公租自行车数量是2016年底平均每个摆放点的公租自行车数量的1.2倍. 预计到2018年底,全区将有摆放点多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,正方形ABCD中,![]() ,
,![]() 绕点A顺时针旋转,它的两边长分别交CB、DC或它们的延长线
绕点A顺时针旋转,它的两边长分别交CB、DC或它们的延长线![]() 于点MN,
于点MN,![]() 于点H.
于点H.
![]() 如图
如图![]() ,当
,当![]() 点A旋转到
点A旋转到![]() 时,请你直接写出AH与AB的数量关系;
时,请你直接写出AH与AB的数量关系;
![]() 如图
如图![]() ,当
,当![]() 绕点A旋转到
绕点A旋转到![]() 时,
时,![]() 中发现的AH与AB的数量关系还成立吗?如果不成立请写出理由,如果成立请证明.
中发现的AH与AB的数量关系还成立吗?如果不成立请写出理由,如果成立请证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】长城汽车销售公司5月份销售某种型号汽车,当月该型号汽车的进价为30万元/辆,若当月销售量超过5辆时,每多售出1辆,所有售出的汽车进价均降低0.1万元/辆.根据市场调查,月销售量不会突破30台.
(1)设当月该型号汽车的销售量为x辆(x≤30,且x为正整数),实际进价为y万元/辆,求y与x的函数关系式;
(2)已知该型号汽车的销售价为32万元/辆,公司计划当月销售利润45万元,那么该月需售出多少辆汽车?(注:销售利润=销售价﹣进价)
查看答案和解析>>
科目:初中数学 来源: 题型:
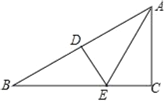
【题目】如图,在△ABC中,∠B=30°,边AB的垂直平分线分别交AB和BC于点D,E,且AE平分∠BAC.
(1)求∠C的度数;
(2)若CE=1,求AB的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com