
【题目】(1)计算下列各题:
①2x2﹣4x+1+2x﹣5x2
②(8x﹣3x2)﹣5xy﹣2(3xy﹣2x2)
(2)先化简,再求值:(3x2y+5x)﹣[x2y﹣4(x﹣x2y)],其中(x+2)2+|y﹣3|=0
【答案】(1)① -3x2-2x+1;② x2-11xy+8x;(2)-2x2y+9x ,-42.
【解析】
(1)①合并同类项即可;②原式去括号然后合并同类项即可;
(2)原式去括号然后合并同类项,然后根据非负数的性质求出x与y的值,代入计算即可.
解:(1)①原式=2x2﹣5x2﹣4x+2x+1= -3x2-2x+1;
②原式=﹣3x2+4x2﹣5xy﹣6xy+8x= x2-11xy+8x;
(2)原式=3x2y+5x﹣x2y+4x-4x2y=-2x2y+9x
![]() (x+2)2+|y﹣3|=0
(x+2)2+|y﹣3|=0
∴x+2=0,y﹣3=0
∴x=-2,y=3
∴原式 =-2×(-2)2×3+9×(-2)=-42.
故答案为:(1)① -3x2-2x+1;② x2-11xy+8x;(2)-2x2y+9x ,-42.


科目:初中数学 来源: 题型:
【题目】(1)甲、乙、丙、丁四人做传球游戏:第一次由甲将球随机传给乙、丙、丁中的某一人,从第二次起,每一次都由持球者将球再随机传给其他三人中的某一人.求第二次传球后球回到甲手里的概率.(请用“画树状图”的方式给出分析过程)
(2)如果甲跟另外n(n≥2)个人做(1)中同样的游戏,那么,第三次传球后球回到甲手里的概率是 (请直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,下列图案均是长度相同的火柴按一定的规律拼搭而成:第1个图案需7根火柴,第2个图案需13根火柴,…,依此规律,第11个图案需( )根火柴.

A. 156 B. 157 C. 158 D. 159
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习“用直尺和圆规作一个角等于已知角”时,教科书介绍如图:对于“想一想”中的问题,下列回答正确的是( )

A. 根据“边边边”可知,△C′O′D′≌△COD,所以∠A′O′B′=∠AOB
B. 根据“边角边”可知,△C′O′D′≌△COD,所以∠A′O′B′=∠AOB
C. 根据“角边角”可知,△C′O′D′≌△COD,所以∠A′O′B′=∠AOB
D. 根据“角角边”可知,△C′O′D′≌△COD,所以∠A′O′B′=∠AOB
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O为直线AB上一点,∠COE=90°,OF平分∠AOE.
(1)若∠COF=40°,求∠BOE的度数.
(2)若∠COF=α(0°<α<90°),则∠BOE=______(用含α的式子表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】陆老师去水果批发市场采购苹果,他看中了A,B两家苹果,这两家苹果品质一样,零售价都我6元/千克,批发价各不相同.
A家规定:批发数量不超过1000千克,按零售价的92%优惠;批发数量不超过2000千克,按零售价的90%优惠;超过2000千克的按零售价的88%优惠.
B家的规定如下表:
数量范围(千克) | 0~500部分 | 500以上~1500 | 1500以上~2500部分 | 2500以上部分 |
价格补贴 | 零售价的95% | 零售价的85% | 零售价的75% | 零售价的70% |
(1)如果他批发700千克苹果,则他在A、B两家批发分别需要多少元?
(2)如果他批发x千克苹果(1500<x<2000),请你分别用含x的代数式表示他在A、B两家批发所需的费用;
(3)A、B两店在互相竞争中开始了互怼,B说A店的苹果总价有不合理的,有时候买的少反而贵,忽悠消费者;A说B的总价计算太麻烦,把消费者都弄糊涂了;旁边陆老师听完,提出两个问题希望同学们帮忙解决:
问题1:能否举例说明A店买的多反而便宜?
问题2:B店老板比较聪明,在平时工作中发现有巧妙的方法:总价=购买数量×单价+价格补贴;
注:不同的单价,补贴价格也不同;只需提前算好即可填下表:
数量范围(千克) | 0~500部分 | 500以上~1500 | 1500以上~2500 | 2500以上部分 |
价格补贴 | 0元 | 300 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,七巧板由图中标号为“![]() ”、“
”、“![]() ”、“
”、“![]() ”、“
”、“![]() ”、“
”、“![]() ”、“
”、“![]() ”、“
”、“![]() ”的七块板组成,七巧板是我们祖先的一项卓越创造,被称为“东方魔板”,它虽然仅有七块板组成,但用它们可以拼出各种各样的图形.请你按下列要求画出所拼的图,图中往上标号:
”的七块板组成,七巧板是我们祖先的一项卓越创造,被称为“东方魔板”,它虽然仅有七块板组成,但用它们可以拼出各种各样的图形.请你按下列要求画出所拼的图,图中往上标号:

①用其中的四块板拼成一个三角形;
②用其中的五块板拼成一个正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是一块锐角三角形材料,高线AH长8cm,底边BC长10cm,要把它加工成一个矩形零件,使矩形DEFG的一边EF在BC上,其余两个顶点D、G分别在AB、AC上,AH交DG于M.
(1)求证:AMBC=AHDG;
(2)加工成的矩形零件DEFG的面积能否等于25cm2?若能,求出宽DE的长度;否则,请说明理由.
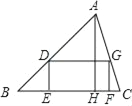
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:a是单项式-xy2的系数,b是最小的正整数,c是多项式2m2n-m3n2-m-2的次数.请回答下列问题:
(1)请直接写出a、b、c的值.a= ,b= ,c= .
(2)数轴上,a、b、c三个数所对应的点分别为A、B、C,点A、B、C同时开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒1个单位长度和3个单位长度的速度向右运动,假设t秒钟过后,若点B与点c之间的距离表示为BC,点A与点C之间的距离表示为AC,点A与点C之间的距离表示为AC.
①t秒钟过后,AC的长度为 (用含t的关系式表示);
②请问:BC-AB的值是否会随着时间t的变化而改变?若变化,请说明理由;若不变,请求出其值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com