
【题目】陆老师去水果批发市场采购苹果,他看中了A,B两家苹果,这两家苹果品质一样,零售价都我6元/千克,批发价各不相同.
A家规定:批发数量不超过1000千克,按零售价的92%优惠;批发数量不超过2000千克,按零售价的90%优惠;超过2000千克的按零售价的88%优惠.
B家的规定如下表:
数量范围(千克) | 0~500部分 | 500以上~1500 | 1500以上~2500部分 | 2500以上部分 |
价格补贴 | 零售价的95% | 零售价的85% | 零售价的75% | 零售价的70% |
(1)如果他批发700千克苹果,则他在A、B两家批发分别需要多少元?
(2)如果他批发x千克苹果(1500<x<2000),请你分别用含x的代数式表示他在A、B两家批发所需的费用;
(3)A、B两店在互相竞争中开始了互怼,B说A店的苹果总价有不合理的,有时候买的少反而贵,忽悠消费者;A说B的总价计算太麻烦,把消费者都弄糊涂了;旁边陆老师听完,提出两个问题希望同学们帮忙解决:
问题1:能否举例说明A店买的多反而便宜?
问题2:B店老板比较聪明,在平时工作中发现有巧妙的方法:总价=购买数量×单价+价格补贴;
注:不同的单价,补贴价格也不同;只需提前算好即可填下表:
数量范围(千克) | 0~500部分 | 500以上~1500 | 1500以上~2500 | 2500以上部分 |
价格补贴 | 0元 | 300 |
【答案】(1)A、B两家批发分别需要3864,3870元;(2)A:5.4x B:4.5x+1200;(3)问题1:见解析,问题2:1200 1950
【解析】
(1)A家批发需要费用:质量×单价×92%;B家批发需要费用:500×单价×95%+(700-500)×单价×85%;把相关数值代入求解即可;
(2)根据“A家批发需要费用:质量×单价×92%;B家批发需要费用:500×单价×95%+1000×单价×85%+(x-1500)×单价×75%”;
(3)①当他要批发超过500千克但不超过1000千克苹果时,设批发x千克苹果,则A家费用=92%×6x=5.52x,B家费用=6×95%×500+6×85%×(x-500)=5.1x+300,A家费用-B家费用=0.42x-300;即可举例说明A店买的多反而便宜;②分别求出B家批发各个价格所需要的费用的等式即可求解.
解:(1)A家:700×6×92%=3864元,
B家:500×6×95%+200×6×85%=3870元;
(2)A家:6x×90%=5.4x,
B家:500×6×95%+1000×6×85%+(x-1500)×6×75%=4.5x+1200;
(3)①当他要批发不超过500千克苹果时,很明显在A家批发更优惠;
当他要批发超过500千克但不超过1000千克苹果时,
设批发x千克苹果,则A家费用=92%×6x=5.52x,B家费用=6×95%×500+6×85%×(x-500)=5.1x+300,
A家费用-B家费用=0.42x-300,要使A店买的多反而便宜即是0.42x-300>0,解得:x>![]()
∴当x>![]() 时,A店买的多反而便宜;
时,A店买的多反而便宜;
②当购买数量为1500以上~2500时,B家需要的总价=500×6×95%+1000×6×85%+(x-1500)×6×75%=4.5x+1200
又![]() 总价=购买数量×单价+价格补贴
总价=购买数量×单价+价格补贴
∴价格补贴=1200元,
当购买数量为2500以上部分时,B家需要的总价=500×6×95%+1000×6×85%+(2500-1500)×6×75%+(x-2500)×6×70%=4.2x+1950
∴价格补贴=1950元.


科目:初中数学 来源: 题型:
【题目】计算:
(1)(-12)-(20)+(-8)-15.
(2)-![]() )3;
)3;
(3)-30×(![]() );
);
(4)(-6)2×(![]() )-22;
)-22;
(5)19![]() +(-1.5)÷(-3)2.
+(-1.5)÷(-3)2.
(6)2![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)计算下列各题:
①2x2﹣4x+1+2x﹣5x2
②(8x﹣3x2)﹣5xy﹣2(3xy﹣2x2)
(2)先化简,再求值:(3x2y+5x)﹣[x2y﹣4(x﹣x2y)],其中(x+2)2+|y﹣3|=0
查看答案和解析>>
科目:初中数学 来源: 题型:
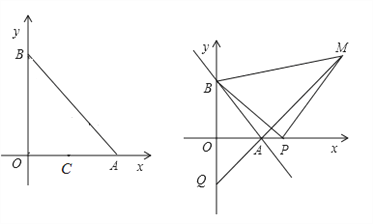
【题目】如图,直线AB交x轴正半轴于点A(a,0),交y轴正半轴于点B(0,b),且a、b满足![]()
(1)求A、B两点的坐标;
(2)C为OA的中点,作点C关于y轴的对称点D,以BD为直角边在第二象限作等腰Rt△BDE,过点E作EF⊥x轴于点F.若直线y=kx-4k将四边形OBEF分为面积相等的两部分,求k的值;
(3)如图,P为x轴上A点右侧任意一点,以BP为边作等腰Rt△PBM,其中PB=PM,直线MA交y轴于点Q,当点P在x轴上运动时,线段OQ的长是否发生变化?若不变,求其值;若变化,求线段OQ的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为缓解城市汽车交通拥堵,减少汽车尾气对大气的污染. 某区政府投放了大量公租自行车供市民使用. 到2016年底,全区已有公租自行车2 500辆,摆放点60个. 预计到2018年底,全区将有公租自行车5 000辆,并且平均每个摆放点的公租自行车数量是2016年底平均每个摆放点的公租自行车数量的1.2倍. 预计到2018年底,全区将有摆放点多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近几年兴义市加大中职教育投入力度,取得了良好的社会效果。某校随机调查了九年级a名学生升学意向,并根据调查结果绘制如图的两幅不完整的统计图。
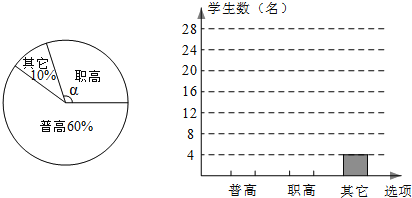
请你根据图中信息解答下列问题:
(1)a= ;
(2)扇形统计图中,“职高”对应的扇形的圆心角α= ;
(3)请补全条形统计图;
(4)若该校九年级有学生900名,估计该校共有多少名毕业生的升学意向是职高。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com