
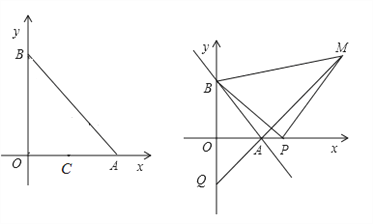
【题目】如图,直线AB交x轴正半轴于点A(a,0),交y轴正半轴于点B(0,b),且a、b满足![]()
(1)求A、B两点的坐标;
(2)C为OA的中点,作点C关于y轴的对称点D,以BD为直角边在第二象限作等腰Rt△BDE,过点E作EF⊥x轴于点F.若直线y=kx-4k将四边形OBEF分为面积相等的两部分,求k的值;
(3)如图,P为x轴上A点右侧任意一点,以BP为边作等腰Rt△PBM,其中PB=PM,直线MA交y轴于点Q,当点P在x轴上运动时,线段OQ的长是否发生变化?若不变,求其值;若变化,求线段OQ的取值范围.
【答案】(1)A(4,0),B(0,4);(2)k值为![]() 或-
或-![]() 或
或![]() ;(3)见解析
;(3)见解析
【解析】(1)首先根据已知条件和非负数的性质得到关于a、b的方程,解方程组即可求出a,b的值,也就能写出A,B的坐标;
(2)先判段出△DEF≌△BDO,得出EF、OF,即可求出四边形OBEF的面积为18,再分析两种情况可讨论计算即可.
(3)过M作x轴的垂线,通过证明△PBO≌△MPN得出MN=AN,转化到等腰直角三角形中即可得出结论.
解:(1)∵![]() ,
,
∴a=4,b=4,
∴A(4,0),B(0,4);
(2)由(1)知,B(0,4);
∴OB=4,
∵C为OA的中点,
∴C(2,0),
∵点C关于y轴的对称点D,
∴D(-2,0)
∴OD=2,
∵BD为直角边在第二象限作等腰Rt△BDE,
①如图,

当BD=BE,∠DBE=90°时,过点E作EH⊥OB于H,
∴∠BHE=90°,
∴∠BEH+∠HBE=90°,
∵∠DBE=90°,
∴∠HBE+∠OBD=90°,
∴∠BEH=∠OBD,
在△OBD和△HEB中,∠BOD=∠EHB=90°,∠0BD=∠BEH,BD=BE,
∴△OBD≌△HEB,
∴BH=OD,EH=OB,
∵D(-2,0),B(0,4),
∴OB=4,OD=2,
∴BH=2,EH=4,
∴OH=OB+BH=6,∴E(-4,6),
∴EF=OH=6,OEH=4,
∴S四边形OBEF=![]() (OB+EF)×OF=20,
(OB+EF)×OF=20,
∵直线y=kx-4k将四边形OBEF分为面积相等的两部分,
∴S四边形OBGF=![]() S四边形OBEF=10,
S四边形OBEF=10,
∴S四边形OBFE=![]() (FG+OB×OF=
(FG+OB×OF=![]() ×(FG+4)×4=2(FG+4)=10,
×(FG+4)×4=2(FG+4)=10,
∴FG=1,∴G(-4,1)
将G(-4,1)代入直线y=kx-4k,得,1=-4k-4k,
∴k=![]() .
.
②如图1,

当DE=BD,∠BDE=90°时,
∴∠EDF+∠BDO=90°,
∴∠DEF=∠BDO,
在△DEF和△BDO中,∠DEF= ∠BOD=90°,∠DEF=∠BDO,DBD,
∴△DEF≌△BDO,
∴EF=OD=2,DF=OB=4,
∴OF=6,
∴F(-6,2)
∴S四边形OBEF=![]() (EF+OB)×OF=
(EF+OB)×OF=![]() ×(2-4)×6=18,
×(2-4)×6=18,
∵直线y=kx-4k将四边形OBEF分为面积相等的两部分,
所以直线y=kx-4k分成的两部分的面积为9,
∵直线y=kx-4k恒过A(4,0),
∴I、当直线y=kx-4k和线段EF相交,
∴S四边形OHGF=9,
∵H(0,-4k),
∴OH=-4k,
∵G点的横坐标为-6,
∴G(-6,-10k),
∴FG=-10k,
∴S四边形OHGF=![]() (-4k=10k)×6=9.
(-4k=10k)×6=9.
∴k=-![]() ,
,
II、当直线y=kx-4k①和线段EB相交,
∴S△MBN=9,
∵N(0,-4k)
∴BN=4(k+1),
∵B(0,4),E(-6,2),
∴直线BE的解析式为y=![]() x+4②
x+4②
联立①②得,点M的横坐标为![]() ,
,
∴S△MBN=![]() ×4(k+1)×
×4(k+1)×![]() =9,
=9,
∴k=![]() (舍)或k=
(舍)或k=![]() .
.
即:满足条件的k值为![]() 或-
或-![]() 或
或![]() .
.
(3)过M作MN⊥x轴,垂足为N.
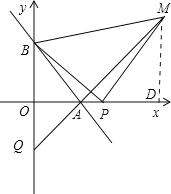
∵∠BPM=90°,∴∠BPO+MPN=90°.
∵∠AOB=∠MNP=90°,∴∠BPO=∠PMN,∠PBO=∠MPN.
∵BP=MP,∴△PBO≌△MPN,
∴ MN=OP,PN=AO=BO,
∴OP=OA+AP=PN+AP=AN,
∴MN=AN,∠MAN=45°.
∵∠BAO=45°,
∴△BAQ是等腰直角三角形.
∴OB=OQ=4.
∴无论P点怎么动,OQ的长不变.
“点睛”此题是一次函数综合题,主要考查了非负性,全等三角形的判定和性质,梯形的面积公式,三角形面积公式,等腰直角三角形的判定和性质,解题关键是求出k的值.


科目:初中数学 来源: 题型:
【题目】根据题意列出方程.
(1)一个数的![]() 与3的差等于最大的一位数,求这个数;
与3的差等于最大的一位数,求这个数;
(2)从正方形的铁皮上,截去2 cm宽的一个长方形条,余下的面积是80 cm2,那么原来的正方形铁皮的边长是多少?
(3)某商店规定,购买超过15 000元的物品可以采用分期付款方式付款,顾客可以先付3 000元,以后每月付1 500元.王叔叔想用分期付款的方式购买价值19 500元的电脑,他需要用多长时间才能付清全部货款?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去….若点A(![]() ,0),B(0,2),则点B2016的坐标为( )
,0),B(0,2),则点B2016的坐标为( )
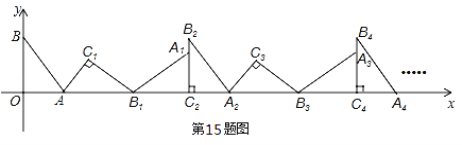
A. (4032 ,2) B. (6048,2) C. (4032,0) D. (6048,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年5月6日,中国第一条具有自主知识产权的长沙磁浮线正式开通运营,该路线连接了长沙火车南站和黄花国际机场两大交通枢纽,沿线生态绿化带走廊的建设尚在进行中,届时将给乘客带来美的享受.星城渣土运输公司承包了某标段的土方运输任务,拟派出大、小两种型号的渣土运输车运输土方,已知2辆大型渣土运输车与3辆小型渣土运输车一次共运输土方31吨,5辆大型渣土运输车与6辆小型渣土运输车一次共运输土方70吨.
(1)一辆大型渣土运输车和一辆小型渣土运输车一次各运输土方多少吨?
(2)该渣土运输公司决定派出大、小两种型号的渣土运输车共20辆参与运输土方,若每次运输土方总量不少于148吨,且小型渣土运输车至少派出2辆,则有哪几种派车方案?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com