
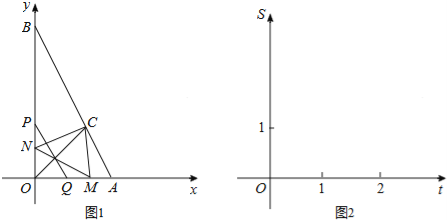
【题目】如图1,已知点A(2,0),B(0,4),∠AOB的平分线交AB于C,一动点P从O点出发,以每秒2个单位长度的速度,沿y轴向点B作匀速运动,过点P且平行于AB的直线交x轴于Q,作P、Q关于直线OC的对称点M、N.设P运动的时间为t(0<t<2)秒.
(1)求C点的坐标,并直接写出点M、N的坐标(用含t的代数式表示);
(2)设△MNC与△OAB重叠部分的面积为S.
①试求S关于t的函数关系式;
②在图2的直角坐标系中,画出S关于t的函数图象,并回答:S是否有最大值?若有,写出S的最大值;若没有,请说明理由.
【答案】(1)(![]() ,
,![]() ),P(0,2t),Q(t,0);(2)①
),P(0,2t),Q(t,0);(2)① ;②当t=1时,S有最大值,最大值为1.
;②当t=1时,S有最大值,最大值为1.
【解析】
试题(1)如答图1,作辅助线,由比例式求出点D的坐标;
(2)①所求函数关系式为分段函数,需要分类讨论:答图2,答图3表示出运动过程中重叠部分(阴影)的变化,分别求解.
②画出函数图象,由两段抛物线构成.观察图象,可知当t=1时,S有最大值.
试题解析:解:(1)如答图1,过点C作CF⊥x轴于点F,CE⊥y轴于点E,
由题意,易知四边形OECF为正方形,设正方形边长为x.
∵CE∥x轴,∴△BEC∽△BOA.∴![]() ,即
,即![]() ,解得x=
,解得x=![]() .
.
∴C点坐标为(![]() ,
,![]() ).
).
∵PQ∥AB,∴![]() ,即
,即![]() .
.
∴OP=2OQ.
∵P(0,2t),∴Q(t,0).
∵对称轴OC为第一象限的角平分线,∴对称点坐标为:M(2t,0),N(0,t).
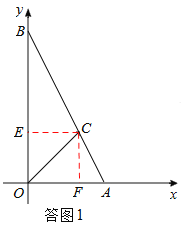
(2)①当0<t≤1时,如答图2所示,点M在线段OA上,重叠部分面积为S△CMN.
S△CMN=S四边形CMON﹣S△OMN=(S△COM+S△CON)﹣S△OMN![]() .
.
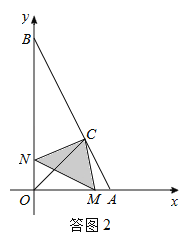
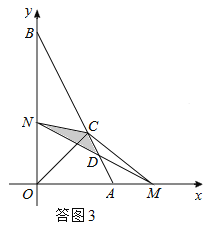
当1<t<2时,如答图3所示,点M在OA的延长线上,
设MN与AB交于点D,则重叠部分面积为S△CDN.
设直线MN的解析式为y=kx+b,
将M(2t,0)、N(0,t)代入得![]() ,解得
,解得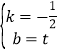 .
.
∴直线MN的解析式为![]() .
.
同理求得直线AB的解析式为:y=﹣2x+4.
联立![]() 与y=﹣2x+4,求得点D的横坐标为
与y=﹣2x+4,求得点D的横坐标为![]() .
.
S△CDN=S△BDN﹣S△BCN=![]() .
.
综上所述,S关于t的函数关系式为 .
.
②画出函数图象,如答图4所示:
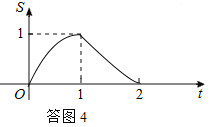
观察图象,可知当t=1时,S有最大值,最大值为1.


科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2-4x+c的图象过点(-1, 0)和点(2,-9).
(1) 求该二次函数的解析式并写出其对称轴;
(2) 已知点P(2 , -2),连结OP , 在x轴上找一点M,使△OPM是等腰三角形,请直接写出点M的坐标(不写求解过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】当m是何值时,关于x的方程(m2+2)x2+(m﹣1)x﹣4=3x2
(1)是一元二次方程;
(2)是一元一次方程;
(3)若x=﹣2是它的一个根,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习掷硬币的概率时,老师说:“掷一枚质地均匀的硬币,正面朝上的概率是![]() ”,小明做了下列三个模拟实验来验证.
”,小明做了下列三个模拟实验来验证.
①取一枚新硬币,在桌面上进行抛掷,计算正面朝上的次数与总次数的比值;
②把一个质地均匀的圆形转盘平均分成偶数份,并依次标上奇数和偶数,转动转盘,计算指针落在奇数区域的次数与总次数的比值;
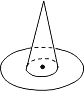
③将一个圆形纸板放在水平的桌面上,纸板正中间放一个圆锥(如图),从圆锥的正上方往下撒米粒,计算其中一半纸板上的米粒数与纸板上总米粒数的比值. 上面的实验中,不科学的有( )
A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校计划在“阳光体育”活动课程中开设乒乓球、羽毛球、篮球、足球四个体育活动项目供学生选择.为了估计全校学生对这四个活动项目的选择情况,体育老师从全体学生中随机抽取了部分学生进行调查(规定每人必须并且只能选择其中的一个项目),并把调查结果绘制成如图所示的不完整的条形统计图和扇形统计图,请你根据图中信息解答下列问题:
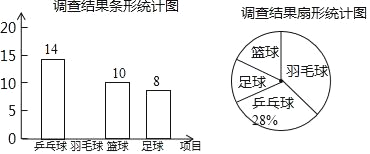
(1)求参加这次调查的学生人数,并补全条形统计图;
(2)求扇形统计图中“篮球”项目所对应扇形的圆心角度数;
(3)若该校共有600名学生,试估计该校选择“足球”项目的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司在羊年春节晚会上举行一个游戏,规则如下:有4张背面相同的卡片,正面分别是喜羊羊、美羊羊、慢羊羊、懒羊羊的头像,分别对应1000元、600元、400元、200元的奖金,现将4张纸牌洗匀后背面朝上摆放到桌上,让员工抽取,每人有两次抽奖机会,两次抽取的奖金之和作为公司发的年终奖金.现有两种抽取的方案:①小芳抽取方案是:直接从四张牌中抽取两张.②小明抽取的方案是:先从四张牌中抽取一张后放回去,再从四张中再抽取一张.你认为是小明抽到的奖金不少于1000元的概率大还是小芳抽取到的奖金不少于1000元的概率大?请用树形图或列表法进行分析说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王勇和李明两位同学在学习“概率”时,做投掷骰子(质地均匀的正方体)实验,他们共做了30次实验,实验的结果如下:
朝上的点数 | 1 | 2 | 3 | 4 | 5 | 6 |
出现的次数 | 2 | 5 | 6 | 4 | 10 | 3 |
(1)分别计算这30次实验中“3点朝上”的频率和“5点朝上”的频率;
(2)王勇说:“根据以上实验可以得出结论:由于5点朝上的频率最大,所以一次实验中出现5点朝上的概率最大”;李明说:“如果投掷300次,那么出现6点朝上的次数正好是30次”.试分别说明王勇和李明的说法正确吗?并简述理由;
(3)现王勇和李明各投掷一枚骰子,请用列表或画树状图的方法求出两枚骰子朝上的点数之和为3的倍数的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com