
ЁОЬтФПЁПЦНУцжБНЧзјБъЯЕxOyжаЃЌЕуAЁЂBЗжБ№дкКЏЪ§y1=![]() ЃЈxЃО0ЃЉгыy2=
ЃЈxЃО0ЃЉгыy2=![]() ЃЈxЃМ0ЃЉЕФЭМЯѓЩЯЃЌAЁЂBЕФКсзјБъЗжБ№ЮЊaЁЂbЃЎ
ЃЈxЃМ0ЃЉЕФЭМЯѓЩЯЃЌAЁЂBЕФКсзјБъЗжБ№ЮЊaЁЂbЃЎ
ЃЈ1ЃЉШєABЁЮxжсЃЌЧѓЁїOABЕФУцЛ§ЃЛ
ЃЈ2ЃЉШєЁїOABЪЧвдABЮЊЕзБпЕФЕШбќШ§НЧаЮЃЌЧвa+b![]() 0ЃЌЧѓabЕФжЕЃЛ
0ЃЌЧѓabЕФжЕЃЛ
ЃЈ3ЃЉзїБпГЄЮЊ3ЕФе§ЗНаЮACDEЃЌЪЙACЁЮxжсЃЌЕуDдкЕуAЕФзѓЩЯЗНЃЌФЧУДЃЌЖдДѓгкЛђЕШгк4ЕФШЮвтЪЕЪ§aЃЌCDБпгыКЏЪ§y1=![]() ЃЈxЃО0ЃЉЕФЭМЯѓЖМгаНЛЕуЃЌЧыЫЕУїРэгЩЃЎ
ЃЈxЃО0ЃЉЕФЭМЯѓЖМгаНЛЕуЃЌЧыЫЕУїРэгЩЃЎ

ЁОД№АИЁПЃЈ1ЃЉSЁїOAB=4ЃЛЃЈ2ЃЉab=Љ4ЃЛЃЈ3ЃЉМћНтЮі.
ЁОНтЮіЁП
ЃЈ1ЃЉШчЭМ1ЃЌABНЛyжсгкCЃЌгЩгкABЁЮxжсЃЌИљОнkЕФМИКЮвтвхЕУЕНSЁїOACЃН2ЃЌSЁїOBCЃН2ЃЌЫљвдSЁїOABЃНSЁїOAC+SЁїOBCЃН4ЃЛ
ЃЈ2ЃЉИљОнКЏЪ§ЭМЯѓЩЯЕуЕФзјБъЬиеїЕУAЁЂBЕФзнзјБъЗжБ№ЮЊ![]() ЃЌИљОнСНЕуМфЕФОрРыЙЋЪНЕУЕН
ЃЌИљОнСНЕуМфЕФОрРыЙЋЪНЕУЕН![]() ЃЌдђРћгУЕШбќШ§НЧаЮЕФаджЪЕУЕНa2+ЃЈ
ЃЌдђРћгУЕШбќШ§НЧаЮЕФаджЪЕУЕНa2+ЃЈ![]() ЃЉ2ЃНb2+ЃЈЉ
ЃЉ2ЃНb2+ЃЈЉ![]() ЃЉ2ЃЌБфаЮЕУЕНЃЈa+bЃЉЃЈaЉbЃЉЃЈ1Љ
ЃЉ2ЃЌБфаЮЕУЕНЃЈa+bЃЉЃЈaЉbЃЉЃЈ1Љ![]() ЃЉЃН0ЃЌгЩгкa+bЁй0ЃЌaЃО0ЃЌbЃМ0ЃЌЫљвд1Љ
ЃЉЃН0ЃЌгЩгкa+bЁй0ЃЌaЃО0ЃЌbЃМ0ЃЌЫљвд1Љ![]() ЃН0ЃЌвзЕУabЃНЉ4ЃЛ
ЃН0ЃЌвзЕУabЃНЉ4ЃЛ
ЃЈ3ЃЉгЩгкaЁн4ЃЌACЃН3ЃЌдђПЩХаЖЯжБЯпCDдкyжсЕФгвВрЃЌжБЯпCDгыКЏЪ§y1ЃН![]() ЃЈxЃО0ЃЉЕФЭМЯѓвЛЖЈгаНЛЕуЃЌЩшжБЯпCDгыКЏЪ§y1ЃН
ЃЈxЃО0ЃЉЕФЭМЯѓвЛЖЈгаНЛЕуЃЌЩшжБЯпCDгыКЏЪ§y1ЃН![]() ЃЈxЃО0ЃЉЕФЭМЯѓНЛЕуЮЊFЃЌгЩгкAЕузјБъЮЊЃЈaЃЌ
ЃЈxЃО0ЃЉЕФЭМЯѓНЛЕуЮЊFЃЌгЩгкAЕузјБъЮЊЃЈaЃЌ![]() ЃЉЃЌе§ЗНаЮACDEЕФБпГЄЮЊ3ЃЌдђЕУЕНCЕузјБъЮЊЃЈaЉ3ЃЌ
ЃЉЃЌе§ЗНаЮACDEЕФБпГЄЮЊ3ЃЌдђЕУЕНCЕузјБъЮЊЃЈaЉ3ЃЌ![]() ЃЉЃЌFЕуЕФзјБъЮЊЃЈaЉ3ЃЌ
ЃЉЃЌFЕуЕФзјБъЮЊЃЈaЉ3ЃЌ![]() ЃЉЃЌЫљвдFCЃН
ЃЉЃЌЫљвдFCЃН![]() ЃЌШЛКѓБШНЯFCгы3ЕФДѓаЁЃЌгЩгк3ЉFCЃН3Љ
ЃЌШЛКѓБШНЯFCгы3ЕФДѓаЁЃЌгЩгк3ЉFCЃН3Љ![]() ЃЌЖјaЁн4ЃЌЫљвд3ЉFCЁн0ЃЌгкЪЧПЩХаЖЯЕуFдкЯпЖЮDCЩЯЃЎ
ЃЌЖјaЁн4ЃЌЫљвд3ЉFCЁн0ЃЌгкЪЧПЩХаЖЯЕуFдкЯпЖЮDCЩЯЃЎ
НтЃКЃЈ1ЃЉШчЭМЃЌABНЛyжсгкPЃЌ
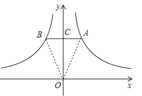
ЁпABЁЮxжсЃЌ
ЁрSЁїOAC=![]() ЁС|4|=2ЃЌSЁїOBC=
ЁС|4|=2ЃЌSЁїOBC=![]() ЁС|Љ4|=2ЃЌ
ЁС|Љ4|=2ЃЌ
ЁрSЁїOAB=SЁїOAC+SЁїOBC=4ЃЛ
ЃЈ2ЃЉЁпAЁЂBЕФКсзјБъЗжБ№ЮЊaЁЂbЃЌ
ЁрOA2=a2+ЃЈ![]() ЃЉ2ЃЌOB2=b2+ЃЈЉ
ЃЉ2ЃЌOB2=b2+ЃЈЉ![]() ЃЉ2ЃЌ
ЃЉ2ЃЌ
ЁпЁїOABЪЧвдABЮЊЕзБпЕФЕШбќШ§НЧаЮЃЌ
ЁрOA=OBЃЌ
Ёрa2+ЃЈ![]() ЃЉ2=b2+ЃЈЉ
ЃЉ2=b2+ЃЈЉ![]() ЃЉ2
ЃЉ2
ЁрЃЈa+bЃЉЃЈaЉbЃЉЃЈ1Љ![]() ЃЉ=0ЃЌ
ЃЉ=0ЃЌ
Ёпa+bЁй0ЃЌaЃО0ЃЌbЃМ0ЃЌ
Ёр1Љ![]() =0ЃЌ
=0ЃЌ
Ёрab=Љ4
ЃЈ3ЃЉЁпaЁн4ЃЌЖјAC=3ЃЌ
ЁржБЯпCDдкyжсЕФгвВрЃЌжБЯпCDгыКЏЪ§y1=![]() ЃЈxЃО0ЃЉЕФЭМЯѓвЛЖЈгаНЛЕуЃЌ
ЃЈxЃО0ЃЉЕФЭМЯѓвЛЖЈгаНЛЕуЃЌ
ЩшжБЯпCDгыКЏЪ§y1=![]() ЃЈxЃО0ЃЉЕФЭМЯѓНЛЕуЮЊFЃЌШчЭМЃЌ
ЃЈxЃО0ЃЉЕФЭМЯѓНЛЕуЮЊFЃЌШчЭМЃЌ
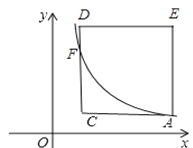
ЁпAЕузјБъЮЊЃЈaЃЌ![]() ЃЉЃЌе§ЗНаЮACDEЕФБпГЄЮЊ3ЃЌ
ЃЉЃЌе§ЗНаЮACDEЕФБпГЄЮЊ3ЃЌ
ЁрCЕузјБъЮЊЃЈaЉ3ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
ЁрFЕуЕФзјБъЮЊЃЈaЉ3ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
ЁрFC=![]() Љ
Љ![]()
Ёп3ЉFC=3Љ![]() ЃЌ
ЃЌ
ЖјaЁн4ЃЌ
Ёр3ЉFCЁн0ЃЌМДFCЁм3ЃЌ
ЁпCD=3ЃЌ
ЁрЕуFдкЯпЖЮDCЩЯЃЌ
МДЖдДѓгкЛђЕШгк4ЕФШЮвтЪЕЪ§aЃЌCDБпгыКЏЪ§y1=![]() ЃЈxЃО0ЃЉЕФЭМЯѓЖМгаНЛЕу
ЃЈxЃО0ЃЉЕФЭМЯѓЖМгаНЛЕу


 дЦФЯЪІДѓИНаЁвЛЯпУћЪІЬсгХзївЕЯЕСаД№АИ
дЦФЯЪІДѓИНаЁвЛЯпУћЪІЬсгХзївЕЯЕСаД№АИ ГхДЬ100ЗжЕЅдЊгХЛЏСЗПМОэЯЕСаД№АИ
ГхДЬ100ЗжЕЅдЊгХЛЏСЗПМОэЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
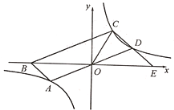
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЦНааЫФБпаЮABCDЕФБпADОЙ§OЕуЃЌAЁЂCЁЂDШ§ЕуЖМдкЗДБШР§КЏЪ§![]() ЕФЭМЯёЩЯЃЌBЕудк
ЕФЭМЯёЩЯЃЌBЕудк![]() жсЕФИКАыжсЩЯЃЌбгГЄCDНЛ
жсЕФИКАыжсЩЯЃЌбгГЄCDНЛ![]() жсгкЕуEЃЌСЌНгCO.
жсгкЕуEЃЌСЌНгCO.
ШєCЃЈ1,2ЃЉ,D(2,1)ЃЌдђ![]() ЮЊ_______.
ЮЊ_______.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
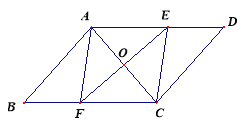
ЁОЬтФПЁПШчЭМЃЌдк![]() ABCDжаЃЌOЪЧЖдНЧЯпACЕФжаЕуЃЌЙ§ЕуOзїACЕФДЙЯпгыБпADЁЂBCЗжБ№НЛгкEЁЂF.ЫФБпаЮAFCEЪЧСтаЮТ№ЃПЧыЫЕУїРэгЩ.
ABCDжаЃЌOЪЧЖдНЧЯпACЕФжаЕуЃЌЙ§ЕуOзїACЕФДЙЯпгыБпADЁЂBCЗжБ№НЛгкEЁЂF.ЫФБпаЮAFCEЪЧСтаЮТ№ЃПЧыЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФуГдЙ§РУцТ№ЃПЪЕМЪЩЯдкзіРУцЕФЙ§ГЬжаОЭЩјЭИзХЪ§бЇжЊЪЖЃКвЛЖЈЬхЛ§ЕФУцЭХзіГЩРУцЃЌУцЬѕЕФзмГЄЖШyЃЈmЃЉЫФУцЬѕЕФДжЯИЃЈКсНиУцЛ§ЃЉSЃЈmm2ЃЉЕФЗДБШР§КЏЪ§ЃЌЦфЭМЯѓШчЭМЫљЪО.
ЃЈ1ЃЉаДГіyгыSЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ2ЃЉЧѓЕБУцЬѕДж1.6 mm2ЪБЃЌУцЬѕЕФзмГЄЖШЪЧЖрЩйУзЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
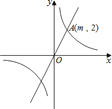
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌе§БШР§КЏЪ§y=kxЕФЭМЯѓгыЗДБШР§КЏЪ§![]() ЕФЭМЯѓгавЛИіНЛЕуAЃЈmЃЌ2ЃЉЃЎ
ЕФЭМЯѓгавЛИіНЛЕуAЃЈmЃЌ2ЃЉЃЎ
ЃЈ1ЃЉЧѓmЕФжЕМАе§БШР§КЏЪ§y=kxЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЪдХаЖЯЕуBЃЈ2ЃЌ3ЃЉЪЧЗёдке§БШР§КЏЪ§ЭМЯѓЩЯЃЌВЂЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
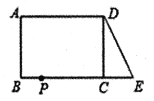
ЁОЬтФПЁПвбжЊЃКШчЭМЃЌдкГЄЗНаЮ![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() .бгГЄ
.бгГЄ![]() ЕНЕу
ЕНЕу![]() ЃЌЪЙ
ЃЌЪЙ![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌЖЏЕу
ЃЌЖЏЕу![]() ДгЕу
ДгЕу![]() ГіЗЂЃЌвдУПУы2ИіЕЅЮЛЕФЫйЖШби
ГіЗЂЃЌвдУПУы2ИіЕЅЮЛЕФЫйЖШби![]() ЯђжеЕу
ЯђжеЕу![]() дЫЖЏЃЌЩшЕу
дЫЖЏЃЌЩшЕу![]() ЕФдЫЖЏЪБМфЮЊ
ЕФдЫЖЏЪБМфЮЊ![]() УыЃЌЕБ
УыЃЌЕБ![]() ЕФжЕЮЊ___________ЪБЃЌ
ЕФжЕЮЊ___________ЪБЃЌ![]() КЭ
КЭ![]() ШЋЕШ.
ШЋЕШ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЫФБпаЮABCDжаЃЌ![]() ЃЌEЮЊBDжаЕуЃЌбгГЄCDЕНЕуFЃЌЪЙ
ЃЌEЮЊBDжаЕуЃЌбгГЄCDЕНЕуFЃЌЪЙ![]() ЃЎ
ЃЎ
![]() ЧѓжЄЃК
ЧѓжЄЃК![]()
![]() ЧѓжЄЃКЫФБпаЮABDFЮЊЦНааЫФБпаЮ
ЧѓжЄЃКЫФБпаЮABDFЮЊЦНааЫФБпаЮ
![]() Шє
Шє![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЧѓЫФБпаЮABDFЕФУцЛ§
ЃЌЧѓЫФБпаЮABDFЕФУцЛ§

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
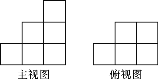
ЁОЬтФПЁПгЩвЛаЉДѓаЁЯрЭЌЕФаЁе§ЗНЬхзщГЩЕФМђЕЅМИКЮЬхЕФжїЪгЭМКЭИЉЪгЭМШчЭМ29-29ЫљЪО.
(1)ЧыФуЛГіетИіМИКЮЬхЕФвЛжжзѓЪгЭМ.
(2)ШєзщГЩетИіМИКЮЬхЕФаЁе§ЗНЬхЕФПщЪ§ЮЊnЃЌЧыФуаДГіnЕФЫљгаПЩФмжЕ.
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com