练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知反比例函数y=（x≠0）的图象经过（3，－1），则当1<y<3时，自变量x的取值范围是______．

    【答案】

    【解析】

    根据反比例函数过点（3，﹣1）结合反比例函数图象上点的坐标特征可求出k值，根据k值可得出反比例函数在每个象限内的函数值y随x增大而增大，代入y=1、y=3求出x值，即可得出结论．

    ∵反比例函数y（k≠0）的图象经过（3，﹣1），∴k=3×（﹣1）=﹣3，∴反比例函数的解析式为y．

    ∵反比例函数y中k=﹣3，∴该反比例函数的图象经过第二、四象限，且在每个象限内函数值y随x增大而增大．

    当y=1时，x3；

    当y=3时，x1，∴1＜y＜3时，自变量x的取值范围是﹣3＜x＜﹣1．

    故答案为：﹣3＜x＜﹣1．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】对任意一个正整数m，如果，其中n是正整数，则称m为“优数”，n为m的最优拆分点，例如：，则72是一个“优数”，8为72的最优拆分点．

    请写出一个大于40小于50的“优数”______，它的最优拆分点是______．

    把“优数”p的2倍与“优数”q的3倍的差记为，例如：，，则若“优数”p的最优拆分点为，“优数”q的最优拆分点为t，当时，求t的值并判断它是否为“优数”．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

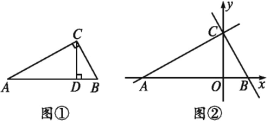
    【题目】如图,在△ABC中,∠ACB=90°,CD⊥AB,

    (1)图①中共有　　　　　对相似三角形,写出来分别为　　　　　　　　　(不需证明);

    (2)已知AB=10,AC=8,请你求出CD的长;

    (3)在(2)的情况下,如果以AB为x轴,CD为y轴,点D为坐标原点O,建立直角坐标系(如图②),若点P从点C出发,以每秒1个单位的速度沿线段CB运动,点Q从点B出发,以每秒1个单位的速度沿线段BA运动,其中一点最先到达线段的端点时,两点即刻同时停止运动;设运动时间为t秒,是否存在点P,使以点B,P,Q为顶点的三角形与△ABC相似?若存在,请求出点P的坐标;若不存在,请说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某手机生产厂家根据其产品在市场上的销售情况，决定对原来以每部2000元出售的一款彩屏手机进行调价，并按新单价的八折优惠出售，结果每部手机仍可获得实际销售价的20%的利润（利润=销售价—成本价）.已知该款手机每部成本价是原销售单价的60%.

    （1）求调整后这款彩屏手机的新单价是每部多少元？让利后的实际销售价是每部多少元？

    （2）为使今年按新单价让利销售的利润不低于20万元，今年至少应销售这款彩屏手机多少部？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

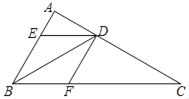
    【题目】如图，BD是△ABC的角平分线，过点D作DE∥BC交AB于点E，DF∥AB交BC于点F．

    （1）求证：四边形BEDF为菱形；

    （2）如果∠A＝90°，∠C＝30°，BD＝6，求菱形BEDF的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

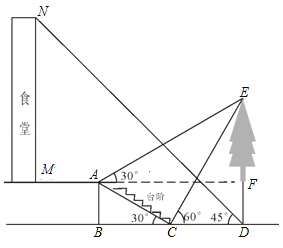
    【题目】（2017湖北省鄂州市）小明想要测量学校食堂和食堂正前方一棵树的高度，他从食堂楼底M处出发，向前走3米到达A处，测得树顶端E的仰角为30°，他又继续走下台阶到达C处，测得树的顶端E的仰角是60°，再继续向前走到大树底D处，测得食堂楼顶N的仰角为45°．已知A点离地面的高度AB=2米，∠BCA=30°，且B、C、D三点在同一直线上．

    （1）求树DE的高度；

    （2）求食堂MN的高度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

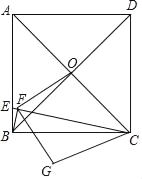
    【题目】如图，正方形ABCD中，AD＝4，E在AB上且AB＝4BE，连接CE，作BF⊥CE于F，正方形对角线交于O点，连接OF，将△COF沿CE翻折得△CGF，连接BG，则BG的长为_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】我市部分学生参加了全国初中数学竞赛决赛，并取得优异成绩．已知竞赛成绩分数都是整数，试题满分为140分，参赛学生的成绩分数分布情况如下：

    分数段

    0-19

    20-39

    40-59

    60-79

    80-99

    100-119

    120-140

    人数

    0

    37

    68

    95

    56

    32

    12

    请根据以上信息解答下列问题：
    （1）全市共有多少人参加本次数学竞赛决赛？最低分和最高分在什么分数范围？
    （2）经竞赛组委会评定，竞赛成绩在60分以上（含60分）的考生均可获得不同等级的奖励，求我市参加本次竞赛决赛考生的获奖比例；
    （3）决赛成绩分数的中位数落在哪个分数段内？
    （4）上表还提供了其他信息，例如：“没获奖的人数为105人”等等．请你再写出两条此表提供的信息．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】将两块斜边长相等的等腰直角三角板按如图①摆放，斜边AB分别交CD，CE于M，N点．

    (1)如果把图①中的△BCN绕点C逆时针旋转90°得到△ACF，连接FM，如图②，求证：△CMF≌△CMN；

    (2)将△CED绕点C旋转，则：

    ①当点M，N在AB上(不与点A，B重合)时，线段AM，MN，NB之间有一个不变的关系式，请你写出这个关系式，并说明理由；

    ②当点M在AB上，点N在AB的延长线上(如图③)时，①中的关系式是否仍然成立？

    查看答案和解析>>

    同步练习册答案