
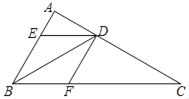
【题目】如图,BD是△ABC的角平分线,过点D作DE∥BC交AB于点E,DF∥AB交BC于点F.
(1)求证:四边形BEDF为菱形;
(2)如果∠A=90°,∠C=30°,BD=6,求菱形BEDF的面积.
【答案】(1)证明见解析;(2)S四边形BEDF=6![]() .
.
【解析】
(1)由题意可证BE=DE,四边形BEDF是平行四边形,即可证四边形BEDF为菱形;
(2)过点D作DH⊥BC于点H,由题意可得BD=CD=6,根据30度所对的直角边等于斜边的一半,可求DH=3,即可求DF=BF的长,即可得菱形BEDF的面积.
(1)∵DE∥BC,DF∥AB,∴四边形DEBF是平行四边形.
∵DE∥BC,∴∠EDB=∠DBF.
∵BD平分∠ABC,∴∠ABD=∠DBF![]() ∠ABC,∴∠ABD=∠EDB,∴DE=BE且四边形BEDF为平行四边形,∴四边形BEDF为菱形.
∠ABC,∴∠ABD=∠EDB,∴DE=BE且四边形BEDF为平行四边形,∴四边形BEDF为菱形.
(2)如图:过点D作DH⊥BC于点H.
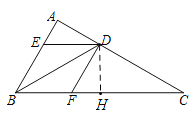
∵∠A=90°,∠C=30°,∴∠ABC=60°,∴∠DBC=30°=∠C,∴DB=DC=6.
∵DH⊥BC,∠C=30°,∴DC=2DH=6,∴DH=3.
∵DF∥AB,∴∠A=∠FDC=90°,且∠C=30°,DC=6,∴DC![]() DF,∴DF=2
DF,∴DF=2![]() .
.
∵四边形BEDF为菱形,∴BF=DF=2![]() ,∴S四边形BEDF=BF×DH=2
,∴S四边形BEDF=BF×DH=2![]() 3=6
3=6![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
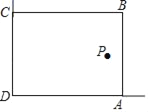
【题目】在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用32m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=xm.
(1)若花园的面积为252m2,求x的值;
(2)若在P处有一棵树与墙CD,AD的距离分别是17m和6m,要将这棵树围在花园内(含边界,不考虑树的粗细),求花园面积S的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级为了解学生课堂发言情况,随机抽取该年级部分学生,对他们某天在课堂上发言的次数进行了统计,其结果如下表,并绘制了如图所示的两幅不完整的统计图,已知B、E两组发言人数的比为5:2,请结合图中相关数据回答下列问题:
(1)则样本容量容量是______________,并补全直方图;
(2)该年级共有学生500人,请估计全年级在这天里发言次数不少于12的次数;
(3)已知A组发言的学生中恰有1位女生,E组发言的学生中有2位男生,现从A组与E组中分别抽一位学生写报告,请用列表法或画树状图的方法,求所抽的两位学生恰好是一男一女的概率。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解永康市某中学八年级学生的视力水平,从中抽查部分学生的视力情况,绘制了如图统计图:
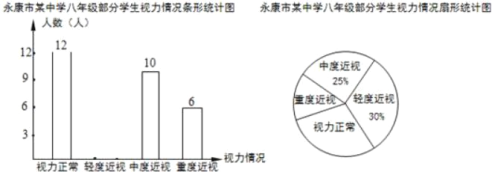
(1)本次调查的样本容量是 ;
(2)请补全条形统计图,并求扇形统计图中“视力正常”的圆心角度数;
(3)该校八年级共有200位学生,请估计该校八年级视力正常的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】行驶中的汽车,在刹车后由于惯性的作用,还要向前方滑行一段距离才能停止,这段距离称为“刹车距离”,为了测定某种型号的汽车的刹车性能(车速不超过140 km/h),对这种汽车进行测试,测得数据如下表:
刹车时车速/km·h-1 | 0 | 10 | 20 | 30 | 40 | 50 | 60 |
刹车距离/m | 0 | 0.3 | 1.0 | 2.1 | 3.6 | 5.5 | 7.8 |
(1)以车速为x轴,以刹车距离为y轴,建立平面直角坐标系,根据上表对应值作出函数的大致图象;
(2)观察图象.估计函数的类型,并确定一个满足这些数据的函数解析式;
(3)该型号汽车在国道发生了一次交通事故,现场测得刹车距离为46.5 m,推测刹车时的车速是多少?请问事故发生时,汽车是超速行驶还是正常行驶?
查看答案和解析>>
科目:初中数学 来源: 题型:
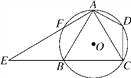
【题目】如图,已知四边形ABCD内接于⊙O,A是![]() 的中点,AE⊥AC于A,与⊙O及CB的延长线交于点F,E,且
的中点,AE⊥AC于A,与⊙O及CB的延长线交于点F,E,且![]() .
.
(1)求证:△ADC∽△EBA;
(2)如果AB=8,CD=5,求tan∠CAD的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OA和OB是⊙O的半径,OB=2,OA⊥OB,P是OA上任一点,BP的延长线交⊙O于点Q,过点Q的⊙O的切线交OA延长线于点R.
(1)求证:RP=RQ;
(2)若OP=PQ,求PQ的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知钝角三角形ABC,将△ABC绕点A按逆时针方向旋转110°得到△AB′C′,连接BB′,若AC′∥BB′,则∠CAB′的度数为( )
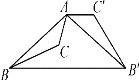
A. 55°B. 65°C. 85°D. 75°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com