
【题目】如图,已知钝角三角形ABC,将△ABC绕点A按逆时针方向旋转110°得到△AB′C′,连接BB′,若AC′∥BB′,则∠CAB′的度数为( )
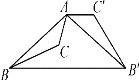
A. 55°B. 65°C. 85°D. 75°
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
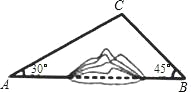
【题目】如图,A,B两地之间有一座山,汽车原来从A地到B地须经C地沿折线A﹣C﹣B行驶,现开通隧道后,汽车直接沿直线AB行驶.已知AC=10km,∠A=30°,∠B=45°,则隧道开通后,汽车从A地到B地比原来少走多少千米?(结果精确到0.1km)(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
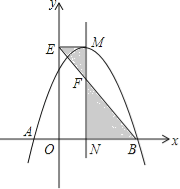
【题目】如图,抛物线![]() 与x轴交于A,B两点,它们的对称轴与x轴交于点N,过顶点M作ME⊥y轴于点E,连结BE交MN于点F.已知点A的坐标为(﹣1,0).
与x轴交于A,B两点,它们的对称轴与x轴交于点N,过顶点M作ME⊥y轴于点E,连结BE交MN于点F.已知点A的坐标为(﹣1,0).
(1)求该抛物线的解析式及顶点M的坐标;
(2)求△EMF与△BNF的面积之比.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】任选一题作答,只计一题的成绩:
一、如图,某工厂![]() 和一条笔直的公路
和一条笔直的公路![]() ,原有两条路
,原有两条路![]() ,
,![]() 可以
可以![]() 到达
到达![]() ,经测量
,经测量![]() ,
,![]() ,
,![]() ,现需要修建一条新公路,使
,现需要修建一条新公路,使![]() 到
到![]() 的距离最短.请你帮
的距离最短.请你帮![]() 设计一种方案,并求新建公路的长.
设计一种方案,并求新建公路的长.

二、如图,![]() ,
,![]()
![]() ,
,![]()
![]() ,
, ![]()
![]() ,
,![]()
![]() .
.
(1)试判断以点![]() ,
,![]() ,
,![]() 为顶点的三角形的形状,并说明理由;
为顶点的三角形的形状,并说明理由;
(2)求该图的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某出租车驾驶员从公司出发,在南北向的人民路上连续接送5批客人,行驶路程记录如下(规定向南为正,向北为负,单位:km):

①接送完第5批客人后,该驾驶员在公司什么方向,距离公司多少千米?
②若该出租车每千米耗油0.2升,那么在这过程中共耗油多少升?
③若该出租车的计价标准为:行驶路程不超过3km收费10元,超过3km的部分按每千米加1.8元收费,在这过程中该驾驶员共收到车费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在社会主义新农村建设中,某乡镇决定对一段公路进行改造,已知这项工程由甲工程队单独做需要40天完成;如果由乙工程先单独做10天,那么剩下的工程还需要两队合做20天才能完成.
(1)求乙工程队单独完成这项工程所需的天数;
(2)求两队合作完成这项工程所需的天数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y=mx2-6x+1(m是常数).
(1)求证:不论m为何值,该函数的图象都经过y轴上的一个定点;
(2)若该函数的图象与x轴只有一个交点,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一个长为24米的篱笆,一面利用墙(墙的最大可用长度为10米)围成中间隔有一道篱笆的长方形花圃.设花圃的宽AB为x米,面积为S平方米.
(1)求S与x的函数关系式及x的取值范围;
(2)如果要围成面积为45平方米的花圃,那么AB的长为多少米?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com