
【题目】任选一题作答,只计一题的成绩:
一、如图,某工厂![]() 和一条笔直的公路
和一条笔直的公路![]() ,原有两条路
,原有两条路![]() ,
,![]() 可以
可以![]() 到达
到达![]() ,经测量
,经测量![]() ,
,![]() ,
,![]() ,现需要修建一条新公路,使
,现需要修建一条新公路,使![]() 到
到![]() 的距离最短.请你帮
的距离最短.请你帮![]() 设计一种方案,并求新建公路的长.
设计一种方案,并求新建公路的长.

二、如图,![]() ,
,![]()
![]() ,
,![]()
![]() ,
, ![]()
![]() ,
,![]()
![]() .
.
(1)试判断以点![]() ,
,![]() ,
,![]() 为顶点的三角形的形状,并说明理由;
为顶点的三角形的形状,并说明理由;
(2)求该图的面积.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】自主学习,请阅读下列解题过程.
解一元二次不等式:x2﹣5x>0.
解:设x2﹣5x=0,解得:x1=0,x2=5,则抛物线y=x2﹣5x与x轴的交点坐标为(0,0)和(5,0).画出二次函数y=x2﹣5x的大致图象(如图所示),由图象可知:当x<0,或x>5时函数图象位于x轴上方,此时y>0,即x2﹣5x>0,所以,一元二次不等式x2﹣5x>0的解集为:x<0,或x>5.
通过对上述解题过程的学习,按其解题的思路和方法解答下列问题:
(1)上述解题过程中,渗透了下列数学思想中的 和 .(只填序号)
①转化思想 ②分类讨论思想 ③数形结合思想
(2)一元二次不等式x2﹣5x<0的解集为 .
(3)用类似的方法解一元二次不等式:x2﹣2x﹣3>0.
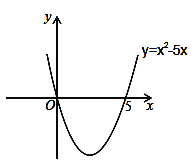
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A、B、C、D、E在同一直线上,且AC=BD,E是线段BC的中点.
![]()
(1)点E是线段AD的中点吗?说明理由;
(2)当AD=10,AB=3时,求线段BE的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
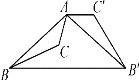
【题目】如图,已知钝角三角形ABC,将△ABC绕点A按逆时针方向旋转110°得到△AB′C′,连接BB′,若AC′∥BB′,则∠CAB′的度数为( )
A. 55°B. 65°C. 85°D. 75°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,要在宽为22米的九州大道两边安装路灯,路灯的灯臂CD长2米,且与灯柱BC成120°角,路灯采用圆锥形灯罩,灯罩的轴线DO与灯臂CD垂直,当灯罩的轴线DO通过公路路面的中心线时照明效果最佳,此时,路灯的灯柱BC高度应该设计为( )

A. (11﹣2![]() )米 B. (11
)米 B. (11![]() ﹣2
﹣2![]() )米 C. (11﹣2
)米 C. (11﹣2![]() )米 D. (11
)米 D. (11![]() ﹣4)米
﹣4)米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,M,N,P,R分别是数轴上的四个整数所对应的点,其中有一个点是原点,并且,MN=NP=PR=1,数a对应的点在M和N之间,数b对应的点在P和R之间,若|a|+|b|=2,则原点是(填M,N,P,R中的一个或几个)_____________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是规格为8×8的正方形网格(小正方形的边长为1,小正方形的顶点叫格点),请在所给网格中按下列要求操作:

(1)请在网格中建立平面直角坐标系,使A点坐标为(-2,4),B点坐标为(-4,2);
(2)按(1)中的直角坐标系在第二象限内的格点上找点C(C点的横坐标大于-3),使点C与线段AB组成一个以AB为底的等腰三角形,则C点坐标是______,△ABC的面积是______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com