
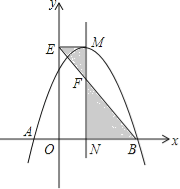
【题目】如图,抛物线![]() 与x轴交于A,B两点,它们的对称轴与x轴交于点N,过顶点M作ME⊥y轴于点E,连结BE交MN于点F.已知点A的坐标为(﹣1,0).
与x轴交于A,B两点,它们的对称轴与x轴交于点N,过顶点M作ME⊥y轴于点E,连结BE交MN于点F.已知点A的坐标为(﹣1,0).
(1)求该抛物线的解析式及顶点M的坐标;
(2)求△EMF与△BNF的面积之比.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案科目:初中数学 来源: 题型:
【题目】阅读材料:求1+2+22+23+24+…+22019的值.
解:设S=1+2+22+23+24+…+22019,将等式两边同时乘以2得:2S=2+22+23+24+25+…+22019+22020
将下式减去上式得2S-S=22020-1
即S=22020-1
即1+2+22+23+24+…=22020-1
请你仿照此法计算:
(1)1+2+22+23+24+…+220
(2)1+5+52+53+54+…+5n(其中n为正整数).
查看答案和解析>>
科目:初中数学 来源: 题型:
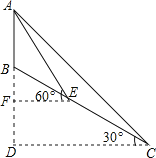
【题目】如图,小山顶上有一信号塔AB,山坡BC的倾角为30°,现为了测量塔高AB,测量人员选择山脚C处为一测量点,测得塔顶仰角为45°,然后顺山坡向上行走100米到达E处,再测得塔顶仰角为60°,求塔高AB.(结果保留整数![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB = AC = 2,∠B =∠C = 50°,点D在线段BC上运动(点D不与B、C重合),连结AD,作∠ADE = 50°,DE交线段AC于点E.
(1)若DC = 2,求证:△ABD≌△DCE;
(2)在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,请求出∠BDA的度数;若不可以,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
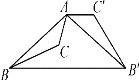
【题目】如图,已知钝角三角形ABC,将△ABC绕点A按逆时针方向旋转110°得到△AB′C′,连接BB′,若AC′∥BB′,则∠CAB′的度数为( )
A. 55°B. 65°C. 85°D. 75°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载.如图1,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图2的方式放置在最大正方形内.若知道图中阴影部分的面积,则一定能求出( )

A.直角三角形的面积
B.最大正方形的面积
C.较小两个正方形重叠部分的面积
D.最大正方形与直角三角形的面积和
查看答案和解析>>
科目:初中数学 来源: 题型:
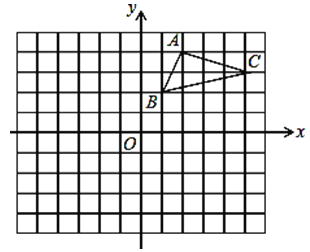
【题目】在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,4)
(1)画出△ABC先向左平移1个单位,再向下平移4个单位得到的△A1B1C1,写出点A1的坐标____________
(2)画出△A1B1C1绕原点O顺时针旋转90°,得到△A2B2C2,写出点A2的坐标_______
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com