
【题目】如图,直线L上有三个正方形a,b,c,若a,c的面积分别为1和9,则b的面积为( )

A.8 B.9 C.10 D.11
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案科目:初中数学 来源: 题型:
【题目】如图,一个正五棱柱的底面边长为2cm,高为4cm。

(1)这个棱柱共有多少个面?计算它的侧面积;
(2)这个棱柱共有多少个顶点?有多少条棱?
(3)试用含有![]() 的代数式表示
的代数式表示![]() 棱柱的顶点数、面数、与棱的条数。
棱柱的顶点数、面数、与棱的条数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A1、A2、A3、…、An在抛物线y=x2图象上,点B1、B2、B3、…、Bn在y轴上,若△A1B0B1、△A2B1B2、…、△AnBn-1Bn都为等腰直角三角形(点B0是坐标原点),则△A2015B2014B2015的腰长=____
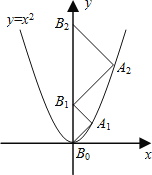
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形![]() 中,将点
中,将点![]() 翻折到对角线
翻折到对角线![]() 上的点
上的点![]() 处,折痕
处,折痕![]() 交
交![]() 于点
于点![]() .将点
.将点![]() 翻折到对角线
翻折到对角线![]() 上的点
上的点![]() 处,折痕
处,折痕![]() 交
交![]() 于点
于点![]() .
.
![]() 求证:四边形
求证:四边形![]() 为平行四边形;
为平行四边形;
![]() 若四边形
若四边形![]() 为菱形,且
为菱形,且![]() ,求
,求![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
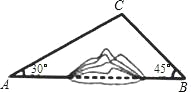
【题目】如图,A,B两地之间有一座山,汽车原来从A地到B地须经C地沿折线A﹣C﹣B行驶,现开通隧道后,汽车直接沿直线AB行驶.已知AC=10km,∠A=30°,∠B=45°,则隧道开通后,汽车从A地到B地比原来少走多少千米?(结果精确到0.1km)(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+b x+c经过A,B,C三点,当x≥0时,其图象如图所示.
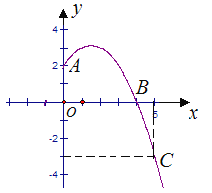
(1)求抛物线的解析式,写出抛物线的顶点坐标;
(2)画出抛物线y=ax2+b x+c当x<0时的图象;
(3)利用抛物线y=ax2+b x+c,写出x为何值时,y>0.
查看答案和解析>>
科目:初中数学 来源: 题型:
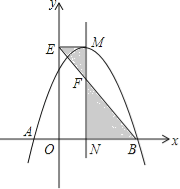
【题目】如图,抛物线![]() 与x轴交于A,B两点,它们的对称轴与x轴交于点N,过顶点M作ME⊥y轴于点E,连结BE交MN于点F.已知点A的坐标为(﹣1,0).
与x轴交于A,B两点,它们的对称轴与x轴交于点N,过顶点M作ME⊥y轴于点E,连结BE交MN于点F.已知点A的坐标为(﹣1,0).
(1)求该抛物线的解析式及顶点M的坐标;
(2)求△EMF与△BNF的面积之比.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某出租车驾驶员从公司出发,在南北向的人民路上连续接送5批客人,行驶路程记录如下(规定向南为正,向北为负,单位:km):

①接送完第5批客人后,该驾驶员在公司什么方向,距离公司多少千米?
②若该出租车每千米耗油0.2升,那么在这过程中共耗油多少升?
③若该出租车的计价标准为:行驶路程不超过3km收费10元,超过3km的部分按每千米加1.8元收费,在这过程中该驾驶员共收到车费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
在数学课上,老师请同学思考如下问题:如图1,我们把一个四边形ABCD的四边中点E,F,G,H依次连接起来得到的四边形EFGH是平行四边形吗?
小敏在思考问题时,有如下思路:连接AC.

结合小敏的思路作答:
(1)若只改变图1中四边形ABCD的形状(如图2),则四边形EFGH还是平行四边形吗?说明理由,参考小敏思考问题的方法解决一下问题;
(2)如图2,在(1)的条件下,若连接AC,BD.
①当AC与BD满足什么条件时,四边形EFGH是菱形,写出结论并证明;
②当AC与BD满足什么条件时,四边形EFGH是矩形,直接写出结论.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com