
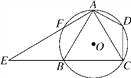
【题目】如图,已知四边形ABCD内接于⊙O,A是![]() 的中点,AE⊥AC于A,与⊙O及CB的延长线交于点F,E,且
的中点,AE⊥AC于A,与⊙O及CB的延长线交于点F,E,且![]() .
.
(1)求证:△ADC∽△EBA;
(2)如果AB=8,CD=5,求tan∠CAD的值.
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() cm,
cm,![]() cm,在
cm,在![]() 中,
中,![]() ,
,![]() cm,
cm,![]() cm.EF在BC上,保持
cm.EF在BC上,保持![]() 不动,并将
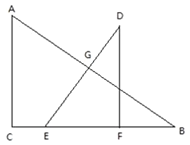
不动,并将![]() 以1cm/s的速度向点C运动,移动开始前点F与点B重合,当点E与点C重合时,
以1cm/s的速度向点C运动,移动开始前点F与点B重合,当点E与点C重合时,![]() 停止移动.边DE与AB相交于点G,连接FG,设移动时间为t(s).
停止移动.边DE与AB相交于点G,连接FG,设移动时间为t(s).
(1)![]() 从移动开始到停止,所用时间为________s;
从移动开始到停止,所用时间为________s;
(2)当DE平分AB时,求t的值;
(3)当![]() 为等腰三角形时,求t的值.
为等腰三角形时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点C在线段AB上,AC=2BC,点D、E在直线AB上,点D在点E的左侧
(1)若AB=18,DE=8,线段DE在线段AB上移动
①如图1,当E为BC中点时,求AD的长;
②点F(异于A,B,C点)在线段AB上,AF=3AD,CE+EF=3,求AD的长;
(2)若AB=2DE,线段DE在直线AB上移动,且满足关系式![]() ,则
,则![]() ______.
______.
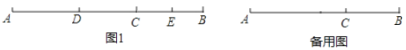
查看答案和解析>>
科目:初中数学 来源: 题型:
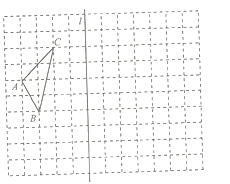
【题目】如图,在![]() 的正方形网格中,
的正方形网格中,![]() 是格点三角形,点
是格点三角形,点![]() 的坐标分别为
的坐标分别为![]() ,
,![]() .
.
(1)在图中画出相应的平面直角坐标系;
(2)画出![]() 关于直线
关于直线![]() 对称的
对称的![]() ,并标出点
,并标出点![]() 的坐标;
的坐标;
(3)若点![]() 在
在![]() 内,其关于直线
内,其关于直线![]() 的对称点是
的对称点是![]() ,则
,则![]() 的坐标是 .
的坐标是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
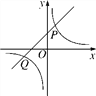
【题目】如图,直线y=k1x+1与双曲线y=![]() 相交于P(1,m),Q(-2,-1)两点.
相交于P(1,m),Q(-2,-1)两点.
(1)求m的值;
(2)若A1(x1,y1),A2(x2,y2),A3(x3,y3)为双曲线上三点,且x1<x2<0<x3,请直接说明y1,y2,y3的大小关系;
(3)观察图象,请直接写出不等式k1x+1>![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
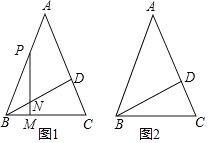
【题目】如图1,在等腰![]() 中,
中,![]() ,点
,点![]() 为边
为边![]() 上一点(不与点
上一点(不与点![]() 、点
、点![]() 重合),
重合),![]() ,垂足为
,垂足为![]() ,交
,交![]() 于点
于点![]() .
.
(1)请猜想![]() 与
与![]() 之间的数量关系,并证明;
之间的数量关系,并证明;
(2)若点![]() 为边
为边![]() 延长线上一点,
延长线上一点,![]() ,垂足为
,垂足为![]() ,交
,交![]() 延长线于点
延长线于点![]() ,请在图2中画出图形,并判断(1)中的结论是否成立.若成立,请证明;若不成立,请写出你的猜想并证明.
,请在图2中画出图形,并判断(1)中的结论是否成立.若成立,请证明;若不成立,请写出你的猜想并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠E=∠F,∠B=∠C,AE=AF,结论:①EM=FN;②CD=DN;③∠FAN=∠EAM;④△ACN≌△ABM.其中正确的有( )
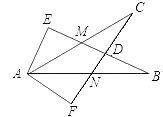
A. 1个B. 2个
C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一个边长为a的正方形分成9个完全相同的小正方形,把最中间的一个小正方形涂成白色(图①),再对其他8个小正方形作同样的分割(分成9个完全相同的小正方形,把最中间的一个小正方形涂成白色(图②),继续同样的方法分割图形(图③),…得到一些既复杂又漂亮的图形,它的每一部分放大,都和整体一模一样,它是波兰数学家谢尔宾斯基构造的,也被称为“谢尔宾斯基地毯”.求:
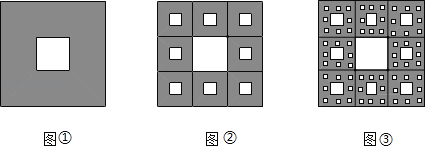
(1)图③中最新的一个最小正方形的边长;
(2)图③中所有涂黑部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
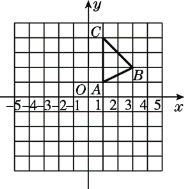
【题目】在平面直角坐标系中,△ABC的三个顶点坐标分别为:A(1,1),B(3,2),C(1,4).
(1)将△ABC先向下平移4个单位,再向右平移1个单位,画出第二次平移后的△A1B1C1.若将△A1B1C1看成是△ABC经过一次平移得到的,则平移距离是________.
(2)以原点为对称中心,画出与△ABC成中心对称的△A2B2C2.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com