
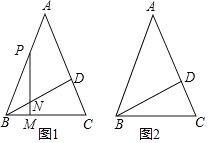
【题目】如图1,在等腰![]() 中,
中,![]() ,点
,点![]() 为边
为边![]() 上一点(不与点
上一点(不与点![]() 、点
、点![]() 重合),
重合),![]() ,垂足为
,垂足为![]() ,交
,交![]() 于点
于点![]() .
.
(1)请猜想![]() 与
与![]() 之间的数量关系,并证明;
之间的数量关系,并证明;
(2)若点![]() 为边
为边![]() 延长线上一点,
延长线上一点,![]() ,垂足为
,垂足为![]() ,交
,交![]() 延长线于点
延长线于点![]() ,请在图2中画出图形,并判断(1)中的结论是否成立.若成立,请证明;若不成立,请写出你的猜想并证明.
,请在图2中画出图形,并判断(1)中的结论是否成立.若成立,请证明;若不成立,请写出你的猜想并证明.
 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:初中数学 来源: 题型:
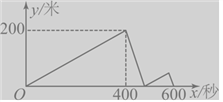
【题目】甲、乙两人在同一直线噵路上同起点,同方向同进出发,分别以不同的速度匀速跑步1500米,当甲超出乙200米时,甲停下来等候乙,甲、乙会合后,两人分别以原来的速度继续跑向终点,先到达终点的人在终点休息,在跑步的整个过程中,甲、乙两人的距离y(米)与出发的时间x(秒)之间的关系如图所示,则甲到终点时,乙距离终点______________米。
查看答案和解析>>
科目:初中数学 来源: 题型:
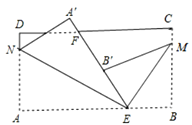
【题目】如图,长方形纸片ABCD,点E,F分别在边AB,CD上,连接EF,将∠BEF对折 B落在直线EF上的点B′处,得折痕EM;将∠AEF对折,点A落在直线EF上的点A′得折痕EN,若∠BEM=62°15′ ,则∠AEN=_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
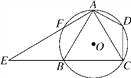
【题目】如图,已知四边形ABCD内接于⊙O,A是![]() 的中点,AE⊥AC于A,与⊙O及CB的延长线交于点F,E,且
的中点,AE⊥AC于A,与⊙O及CB的延长线交于点F,E,且![]() .
.
(1)求证:△ADC∽△EBA;
(2)如果AB=8,CD=5,求tan∠CAD的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,桌上有9张卡片,每张卡片的一面写数字1,另一面写数字-1.每次翻动任意2张(包括已翻过的牌)。改变其向上的面,然后计算能看到的所有牌面数字的积请问, 当翻了2019次时牌面数字的积为( )

A.1B.-1C.2019D.-2019
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=﹣x2+ax+b交x轴于A(1,0),B(3,0)两点,点P是抛物线上在第一象限内的一点,直线BP与y轴相交于点C.
(1)求抛物线y=﹣x2+ax+b的解析式;
(2)当点P是线段BC的中点时,求点P的坐标;
(3)在(2)的条件下,求sin∠OCB的值.
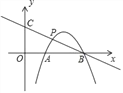
【答案】(1) y=﹣x2+4x﹣3;(2) 点P的坐标为(![]() ,
,![]() );(3)
);(3) ![]() .
.
【解析】分析:(1)将点A、B代入抛物线y=-x2+ax+b,解得a,b可得解析式;
(2)由C点横坐标为0可得P点横坐标,将P点横坐标代入(1)中抛物线解析式,易得P点坐标;
(3)由P点的坐标可得C点坐标,A、B、C的坐标,利用勾股定理可得BC长,利用sin∠OCB=![]() 可得结果.
可得结果.
详解:(1)将点A、B代入抛物线y=﹣x2+ax+b可得,
![]() ,
,
解得,a=4,b=﹣3,
∴抛物线的解析式为:y=﹣x2+4x﹣3;
(2)∵点C在y轴上,
所以C点横坐标x=0,
∵点P是线段BC的中点,
∴点P横坐标xP=![]() =
=![]() ,
,
∵点P在抛物线y=﹣x2+4x﹣3上,
∴yP=![]()
![]() ﹣3=
﹣3=![]() ,
,
∴点P的坐标为(![]() ,
,![]() );
);
(3)∵点P的坐标为(![]() ,
,![]() ),点P是线段BC的中点,
),点P是线段BC的中点,
∴点C的纵坐标为2×![]() ﹣0=
﹣0=![]() ,
,
∴点C的坐标为(0,![]() ),
),
∴BC=![]() =
=![]() ,
,
∴sin∠OCB=![]() =
=![]() =
=![]() .
.
点睛:本题主要考查了待定系数法求二次函数解析式,二次函数图像与性质,解直角三角形,勾股定理,利用中点求得点P的坐标是解答此题的关键.
【题型】解答题
【结束】
24
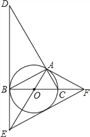
【题目】如图,⊙O是△ABC的外接圆,BC是⊙O的直径,∠ABC=30°,过点B作⊙O的切线BD,与CA的延长线交于点D,与半径AO的延长线交于点E,过点A作⊙O的切线AF,与直径BC的延长线交于点F.
(1)求证:△ACF∽△DAE;
(2)若S△AOC=![]() ,求DE的长;
,求DE的长;
(3)连接EF,求证:EF是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上点A表示数a,点B表示数b,a、b满足|a﹣20|+(b+10)2=0,O是数轴原点,点Q从点B出发,以每秒3个单位长度的速度沿数轴正方向匀速运动,设运动时间为t秒.
![]()
(1)点A表示的数为 ,点B表示的数为 .
(2)t为何值时,BQ=2AQ.
(3)若在点Q从点B出发的同时,点P从点O出发,以每秒2个单位长度的速度一直沿数轴正方向匀速运动,而点Q运动到点A时,立即改变运动方向,沿数轴的负方向运动,到达点B时停止运动,在点Q的整个运动过程中,是否存在合适的t值,使得PQ=6?若存在,求出所有符合条件的t值,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某校为了创建书香校园,去年购进一批图书.经了解,科普书的单价比文学书的单价多4元,用12000元购进的科普书与用8000元购进的文学书本数相等.
(1)文学书和科普书的单价各多少钱?
(2)今年文学书和科普书的单价和去年相比保持不变,该校打算用10000元再购进一批文学书和科普书,问购进文学书550本后至多还能购进多少本科普书?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com