
【题目】如图,在数轴上点A表示数a,点B表示数b,a、b满足|a﹣20|+(b+10)2=0,O是数轴原点,点Q从点B出发,以每秒3个单位长度的速度沿数轴正方向匀速运动,设运动时间为t秒.
![]()
(1)点A表示的数为 ,点B表示的数为 .
(2)t为何值时,BQ=2AQ.
(3)若在点Q从点B出发的同时,点P从点O出发,以每秒2个单位长度的速度一直沿数轴正方向匀速运动,而点Q运动到点A时,立即改变运动方向,沿数轴的负方向运动,到达点B时停止运动,在点Q的整个运动过程中,是否存在合适的t值,使得PQ=6?若存在,求出所有符合条件的t值,若不存在,请说明理由.
【答案】(1)20;﹣10;
(2)当t的值为![]() 或20时,BQ=2AQ.
或20时,BQ=2AQ.
(3)在点Q的整个运动过程中,存在合适的t值,使得PQ=6,t的值为4或![]() .
.
【解析】
(1)利用绝对值及偶次方的非负性,可求出a,b的值,进而可得出结论;
(2)当运动时间为t秒时,在数轴上点Q表示的数为3t-10,结合点A,B表示的数可得出BQ,AQ的值,结合BQ=2AQ,即可得出关于t的一元一次方程,解之即可得出结论;
(3)由点A,B表示的数可求出线段AB的长,结合点Q的运动速度可得出点Q运动到点A的时间及点Q回到点B时的时间,分0<t≤10及10<t≤20两种情况,找出点P,Q表示的数,结合PQ=6,即可得出关于t的一元一次方程,解之即可得出结论.
解:(1)∵|a﹣20|+(b+10)2=0,
∴a﹣20=0,b+10=0,
∴a=20,b=﹣10.
故答案为:20;﹣10.
(2)当运动时间为t秒时,在数轴上点Q表示的数为3t﹣10,
∴BQ=|﹣10﹣(3t﹣10)|=3t,AQ=|20﹣(3t﹣10)|=|30﹣3t|.
∵BQ=2AQ,即3t=2|30﹣3t|,
∴3t=2(30﹣3t)或3t=2(3t﹣30),
解得:t=![]() 或t=20.
或t=20.
答:当t的值为![]() 或20时,BQ=2AQ.
或20时,BQ=2AQ.
(3)AB=|20﹣(﹣10)|=30,
30÷3=10(秒),10×2=20(秒).
当0<t≤10时,在数轴上点Q表示的数为3t﹣10,点P表示的数为2t,
∴PQ=|2t﹣(3t﹣10)|=10﹣t=6,
∴t=4;
当10<t≤20时,在数轴上点Q表示的数为20﹣3(t﹣10)=﹣3t+50,点P表示的数为2t,
∴PQ=|2t﹣(﹣3t+50)|=5t﹣50=6,
解得:t=![]() .
.
答:在点Q的整个运动过程中,存在合适的t值,使得PQ=6,t的值为4或![]() .
.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:
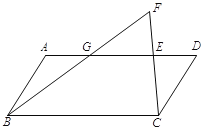
【题目】如图,□ABCD中,∠ABC为锐角,AB<BC,点E是AD上的一点,延长CE到F,连接BF交AD于点G, 使∠FBC=∠DCE.
⑴ 求证:∠D=∠F;
⑵ 在直线AD找一点P,使以点B、P、C为顶点的三角形与以点C、D、P为顶点的三角形相似.(在原图中标出准确P点的位置,必要时用直尺和圆规作出P点,保留作图的痕迹,不写作法)
查看答案和解析>>
科目:初中数学 来源: 题型:
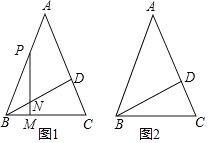
【题目】如图1,在等腰![]() 中,
中,![]() ,点
,点![]() 为边
为边![]() 上一点(不与点
上一点(不与点![]() 、点
、点![]() 重合),
重合),![]() ,垂足为
,垂足为![]() ,交
,交![]() 于点
于点![]() .
.
(1)请猜想![]() 与
与![]() 之间的数量关系,并证明;
之间的数量关系,并证明;
(2)若点![]() 为边
为边![]() 延长线上一点,
延长线上一点,![]() ,垂足为
,垂足为![]() ,交
,交![]() 延长线于点
延长线于点![]() ,请在图2中画出图形,并判断(1)中的结论是否成立.若成立,请证明;若不成立,请写出你的猜想并证明.
,请在图2中画出图形,并判断(1)中的结论是否成立.若成立,请证明;若不成立,请写出你的猜想并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠BAC=54°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠OEC=_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一个边长为a的正方形分成9个完全相同的小正方形,把最中间的一个小正方形涂成白色(图①),再对其他8个小正方形作同样的分割(分成9个完全相同的小正方形,把最中间的一个小正方形涂成白色(图②),继续同样的方法分割图形(图③),…得到一些既复杂又漂亮的图形,它的每一部分放大,都和整体一模一样,它是波兰数学家谢尔宾斯基构造的,也被称为“谢尔宾斯基地毯”.求:
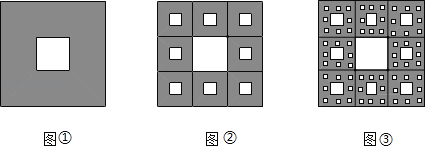
(1)图③中最新的一个最小正方形的边长;
(2)图③中所有涂黑部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A、O、B三点在同一条直线上,OD平分∠AOC,OE平分∠BOC.

(1)若∠BOC=62°,求∠DOE的度数;
(2)若∠BOC=a°,求∠DOE的度数;
(3)图中是否有互余的角?若有请写出所有互余的角.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx﹣3经过点A(2,﹣3),与x轴负半轴交于点B,与y轴交于点C,且OC=3OB.
(1)求抛物线的解析式;
(2)点D在y轴上,且∠BDO=∠BAC,求点D的坐标;
(3)点M在抛物线上,点N在抛物线的对称轴上,是否存在以点A,B,M,N为顶点的四边形是平行四边形?若存在,求出所有符合条件的点M的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
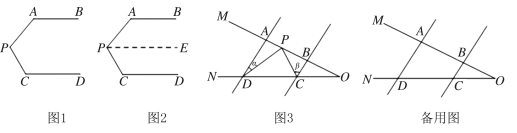
【题目】问题情景:如图1,AB∥CD,∠PAB=130°,∠PCD=120°,求∠APC的度数.
(1)数学活动小组经过讨论形成下列推理,请你补全推理依据.
如图2,过点P作PE∥AB,
∵PE∥AB(作图知)
又∵AB∥CD,
∴PE∥CD.( )
∴∠A+∠APE=180°.
∠C+∠CPE=180°.( )
∵∠PAB=130°,∠PCD=120°,
∴∠APE=50°,∠CPE=60°
∴∠APC=∠APE+∠CPE=110°.
问题迁移:
(2)如图3,AD∥BC,当点P在A、B两点之间运动时,∠ADP=α,∠BCP=β,求∠CPD与α、β之间有何数量关系?请说明理由.
问题解决:
(3)在(2)的条件下,如果点P在A、B两点外侧运动时(点P与点A、B、O三点不重合),请你直接写出∠CPD与α、β之间的数量关系 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com