
ЁОЬтФПЁПШчЭМЃЌАбвЛИіБпГЄЮЊaЕФе§ЗНаЮЗжГЩ9ИіЭъШЋЯрЭЌЕФаЁе§ЗНаЮЃЌАбзюжаМфЕФвЛИіаЁе§ЗНаЮЭПГЩАзЩЋЃЈЭМЂйЃЉЃЌдйЖдЦфЫћ8ИіаЁе§ЗНаЮзїЭЌбљЕФЗжИюЃЈЗжГЩ9ИіЭъШЋЯрЭЌЕФаЁе§ЗНаЮЃЌАбзюжаМфЕФвЛИіаЁе§ЗНаЮЭПГЩАзЩЋЃЈЭМЂкЃЉЃЌМЬајЭЌбљЕФЗНЗЈЗжИюЭМаЮЃЈЭМЂлЃЉЃЌЁЕУЕНвЛаЉМШИДдггжЦЏССЕФЭМаЮЃЌЫќЕФУПвЛВПЗжЗХДѓЃЌЖМКЭећЬхвЛФЃвЛбљЃЌЫќЪЧВЈРМЪ§бЇМваЛЖћБіЫЙЛљЙЙдьЕФЃЌвВБЛГЦЮЊЁАаЛЖћБіЫЙЛљЕиЬКЁБЃЎЧѓЃК
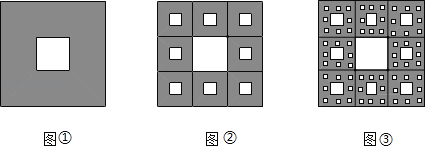
ЃЈ1ЃЉЭМЂлжазюаТЕФвЛИізюаЁе§ЗНаЮЕФБпГЄЃЛ
ЃЈ2ЃЉЭМЂлжаЫљгаЭПКкВПЗжЕФУцЛ§ЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() aЃЛЃЈ2ЃЉ
aЃЛЃЈ2ЃЉ![]() a2ЃЎ
a2ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЙлВьЭМаЮЕФБфЛЏЃКУПЗжИювЛДЮаТЕФе§ЗНаЮЕФБпГЄЪЧЩЯвЛИіе§ЗНаЮБпГЄЕФ![]() ЃЌАДДЫЙцТЩМДПЩЧѓНтЃЛ
ЃЌАДДЫЙцТЩМДПЩЧѓНтЃЛ
ЃЈ2ЃЉЙлВьЭМаЮЕФБфЛЏЃКЭМЂйжаЭПКкВПЗжЫљгае§ЗНаЮЕФУцЛ§ЪЧ![]() aЃЌЭМЂкжаЭПКкВПЗжЫљгае§ЗНаЮЕФУцЛ§ЮЊЃЈ
aЃЌЭМЂкжаЭПКкВПЗжЫљгае§ЗНаЮЕФУцЛ§ЮЊЃЈ![]() ЃЉ2a2ЃЌНјЖјЧѓНтЃЎ
ЃЉ2a2ЃЌНјЖјЧѓНтЃЎ
НтЃКЃЈ1ЃЉЙлВьЭМаЮЕФБфЛЏПЩжЊЃК
УПЗжИювЛДЮЃЌаТЕФе§ЗНаЮЕФБпГЄЪЧЩЯвЛИіе§ЗНаЮЕФБпГЄЕФ![]() ЃЌ
ЃЌ
ЫљвдЭМЂлжааТЕФвЛИізюаЁЕФе§ЗНаЮЕФБпГЄЮЊ![]() aЃН
aЃН![]() aЃЛ
aЃЛ
Д№ЃКЭМЂлжааТЕФвЛИізюаЁе§ЗНаЮЕФБпГЄЮЊ![]() aЃЛ
aЃЛ
ЃЈ2ЃЉЙлВьЭМаЮЕФБфЛЏПЩжЊЃК
ЭМЂйжаЃЌЭПКкВПЗже§ЗНаЮЕФУцЛ§ЮЊ![]() aЃЌ
aЃЌ
ЭМЂкжаЃЌЭПКкВПЗжЫљгае§ЗНаЮЕФУцЛ§ЮЊЃЈ![]() ЃЉ2a2ЃН
ЃЉ2a2ЃН![]() a2ЃЌ
a2ЃЌ
ЭМЂлжаЃЌЭПКкВПЗжЫљгае§ЗНаЮЕФУцЛ§ЮЊЃЈ![]() ЃЉ3a2ЃН
ЃЉ3a2ЃН![]() a2ЃЎ
a2ЃЎ
Д№ЃКЭМЂлжаЃЌЭПКкВПЗжЫљгае§ЗНаЮЕФУцЛ§ЮЊ![]() a2ЃЎ
a2ЃЎ


 ОйвЛЗДШ§ЕЅдЊЭЌВНЙ§ЙиОэЯЕСаД№АИ
ОйвЛЗДШ§ЕЅдЊЭЌВНЙ§ЙиОэЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌХзЮяЯп![]() гы
гы![]() жсНЛгкЕу
жсНЛгкЕу![]() ЃЌгы
ЃЌгы![]() жсНЛгк
жсНЛгк![]() СНЕуЃЌЦфЖдГЦжсгы
СНЕуЃЌЦфЖдГЦжсгы![]() жсНЛгкЕу
жсНЛгкЕу![]() .
.
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНКЭЖдГЦжсЃЛ
ЃЈ2ЃЉдкХзЮяЯпЕФЖдГЦжсЩЯЪЧЗёДцдквЛЕу![]() ЃЌЪЙ
ЃЌЪЙ![]() ЕФжмГЄзюаЁЃПШєДцдкЃЌЧыЧѓГіЕу
ЕФжмГЄзюаЁЃПШєДцдкЃЌЧыЧѓГіЕу![]() ЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
ЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ3ЃЉСЌНг![]() ЃЌдкжБЯп
ЃЌдкжБЯп![]() ЕФЯТЗНЕФХзЮяЯпЩЯЃЌЪЧЗёДцдквЛЕу
ЕФЯТЗНЕФХзЮяЯпЩЯЃЌЪЧЗёДцдквЛЕу![]() ЃЌЪЙ
ЃЌЪЙ![]() ЕФУцЛ§зюДѓЃПШєДцдкЃЌЧыЧѓГіЕу
ЕФУцЛ§зюДѓЃПШєДцдкЃЌЧыЧѓГіЕу![]() ЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
ЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
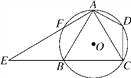
ЁОЬтФПЁПШчЭМЃЌвбжЊЫФБпаЮABCDФкНггкЁбOЃЌAЪЧ![]() ЕФжаЕуЃЌAEЁЭACгкAЃЌгыЁбOМАCBЕФбгГЄЯпНЛгкЕуFЃЌEЃЌЧв
ЕФжаЕуЃЌAEЁЭACгкAЃЌгыЁбOМАCBЕФбгГЄЯпНЛгкЕуFЃЌEЃЌЧв![]() .
.
(1)ЧѓжЄЃКЁїADCЁзЁїEBAЃЛ
(2)ШчЙћABЃН8ЃЌCDЃН5ЃЌЧѓtanЁЯCADЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
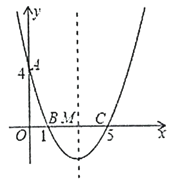
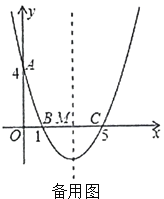
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌХзЮяЯпy=Љx2+ax+bНЛxжсгкAЃЈ1ЃЌ0ЃЉЃЌBЃЈ3ЃЌ0ЃЉСНЕуЃЌЕуPЪЧХзЮяЯпЩЯдкЕквЛЯѓЯоФкЕФвЛЕуЃЌжБЯпBPгыyжсЯрНЛгкЕуCЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпy=Љx2+ax+bЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЕБЕуPЪЧЯпЖЮBCЕФжаЕуЪБЃЌЧѓЕуPЕФзјБъЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌЧѓsinЁЯOCBЕФжЕЃЎ
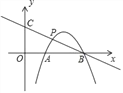
ЁОД№АИЁП(1) y=Љx2+4xЉ3ЃЛ(2) ЕуPЕФзјБъЮЊЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЛ(3)
ЃЉЃЛ(3) ![]() .
.
ЁОНтЮіЁПЗжЮіЃКЃЈ1ЃЉНЋЕуAЁЂBДњШыХзЮяЯпy=-x2+ax+bЃЌНтЕУaЃЌbПЩЕУНтЮіЪНЃЛ
ЃЈ2ЃЉгЩCЕуКсзјБъЮЊ0ПЩЕУPЕуКсзјБъЃЌНЋPЕуКсзјБъДњШыЃЈ1ЃЉжаХзЮяЯпНтЮіЪНЃЌвзЕУPЕузјБъЃЛ
ЃЈ3ЃЉгЩPЕуЕФзјБъПЩЕУCЕузјБъЃЌAЁЂBЁЂCЕФзјБъЃЌРћгУЙДЙЩЖЈРэПЩЕУBCГЄЃЌРћгУsinЁЯOCB=![]() ПЩЕУНсЙћЃЎ
ПЩЕУНсЙћЃЎ
ЯъНтЃКЃЈ1ЃЉНЋЕуAЁЂBДњШыХзЮяЯпy=Љx2+ax+bПЩЕУЃЌ
![]() ЃЌ
ЃЌ
НтЕУЃЌa=4ЃЌb=Љ3ЃЌ
ЁрХзЮяЯпЕФНтЮіЪНЮЊЃКy=Љx2+4xЉ3ЃЛ
ЃЈ2ЃЉЁпЕуCдкyжсЩЯЃЌ
ЫљвдCЕуКсзјБъx=0ЃЌ
ЁпЕуPЪЧЯпЖЮBCЕФжаЕуЃЌ
ЁрЕуPКсзјБъxP=![]() =
=![]() ЃЌ
ЃЌ
ЁпЕуPдкХзЮяЯпy=Љx2+4xЉ3ЩЯЃЌ
ЁрyP=![]()
![]() Љ3=
Љ3=![]() ЃЌ
ЃЌ
ЁрЕуPЕФзјБъЮЊЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЛ
ЃЉЃЛ
ЃЈ3ЃЉЁпЕуPЕФзјБъЮЊЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌЕуPЪЧЯпЖЮBCЕФжаЕуЃЌ
ЃЉЃЌЕуPЪЧЯпЖЮBCЕФжаЕуЃЌ
ЁрЕуCЕФзнзјБъЮЊ2ЁС![]() Љ0=
Љ0=![]() ЃЌ
ЃЌ
ЁрЕуCЕФзјБъЮЊЃЈ0ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
ЁрBC=![]() =
=![]() ЃЌ
ЃЌ
ЁрsinЁЯOCB=![]() =
=![]() =
=![]() ЃЎ
ЃЎ
ЕуОІЃКБОЬтжївЊПМВщСЫД§ЖЈЯЕЪ§ЗЈЧѓЖўДЮКЏЪ§НтЮіЪНЃЌЖўДЮКЏЪ§ЭМЯёгыаджЪЃЌНтжБНЧШ§НЧаЮЃЌЙДЙЩЖЈРэЃЌРћгУжаЕуЧѓЕУЕуPЕФзјБъЪЧНтД№ДЫЬтЕФЙиМќЃЎ
ЁОЬтаЭЁПНтД№Ьт
ЁОНсЪјЁП
24
ЁОЬтФПЁПШчЭМЃЌЁбOЪЧЁїABCЕФЭтНгдВЃЌBCЪЧЁбOЕФжБОЖЃЌЁЯABC=30ЁуЃЌЙ§ЕуBзїЁбOЕФЧаЯпBDЃЌгыCAЕФбгГЄЯпНЛгкЕуDЃЌгыАыОЖAOЕФбгГЄЯпНЛгкЕуEЃЌЙ§ЕуAзїЁбOЕФЧаЯпAFЃЌгыжБОЖBCЕФбгГЄЯпНЛгкЕуFЃЎ
ЃЈ1ЃЉЧѓжЄЃКЁїACFЁзЁїDAEЃЛ
ЃЈ2ЃЉШєSЁїAOC=![]() ЃЌЧѓDEЕФГЄЃЛ
ЃЌЧѓDEЕФГЄЃЛ
ЃЈ3ЃЉСЌНгEFЃЌЧѓжЄЃКEFЪЧЁбOЕФЧаЯпЃЎ
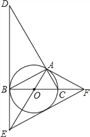
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁбOЪЧЁїABCЕФЭтНгдВЃЌBCЪЧЁбOЕФжБОЖЃЌЁЯABC=30ЁуЃЌЙ§ЕуBзїЁбOЕФЧаЯпBDЃЌгыCAЕФбгГЄЯпНЛгкЕуDЃЌгыАыОЖAOЕФбгГЄЯпНЛгкЕуEЃЌЙ§ЕуAзїЁбOЕФЧаЯпAFЃЌгыжБОЖBCЕФбгГЄЯпНЛгкЕуFЃЎ
ЃЈ1ЃЉЧѓжЄЃКЁїACFЁзЁїDAEЃЛ
ЃЈ2ЃЉШєSЁїAOC=![]() ЃЌЧѓDEЕФГЄЃЛ
ЃЌЧѓDEЕФГЄЃЛ
ЃЈ3ЃЉСЌНгEFЃЌЧѓжЄЃКEFЪЧЁбOЕФЧаЯпЃЎ
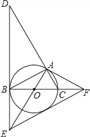
ЁОД№АИЁП(1) МћНтЮі; (2)3![]() ;(3)МћНтЮі.
;(3)МћНтЮі.
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉИљОндВжмНЧЖЈРэЕУЕНЁЯBAC=90ЁуЃЌИљОнШ§НЧаЮЕФФкНЧКЭЕУЕНЁЯACB=60ЁуИљОнЧаЯпЕФаджЪЕУЕНЁЯOAF=90ЁуЃЌЁЯDBC=90ЁуЃЌгкЪЧЕУЕНЁЯD=ЁЯAFC=30ЁугЩЯрЫЦШ§НЧаЮЕФХаЖЈЖЈРэМДПЩЕУЕННсТлЃЛ
ЃЈ2ЃЉИљОнSЁїAOC=![]() ЃЌЕУЕНSЁїACF=
ЃЌЕУЕНSЁїACF=![]() ЃЌЭЈЙ§ЁїACFЁзЁїDAEЃЌЧѓЕУSЁїDAE=
ЃЌЭЈЙ§ЁїACFЁзЁїDAEЃЌЧѓЕУSЁїDAE=![]() ЃЌЙ§AзїAHЁЭDEгкHЃЌНтжБНЧШ§НЧаЮЕУЕНAH=
ЃЌЙ§AзїAHЁЭDEгкHЃЌНтжБНЧШ§НЧаЮЕУЕНAH=![]() DH=
DH=![]() DEЃЌгЩШ§НЧаЮЕФУцЛ§ЙЋЪНСаЗНГЬМДПЩЕУЕННсТлЃЛ
DEЃЌгЩШ§НЧаЮЕФУцЛ§ЙЋЪНСаЗНГЬМДПЩЕУЕННсТлЃЛ
ЃЈ3ЃЉИљОнШЋЕШШ§НЧаЮЕФаджЪЕУЕНOE=OFЃЌИљОнЕШбќШ§НЧаЮЕФаджЪЕУЕНЁЯOFG=![]() ЃЈ180ЁуЉЁЯEOFЃЉ=30ЁуЃЌгкЪЧЕУЕНЁЯAFO=ЁЯGFOЃЌЙ§OзїOGЁЭEFгкGЃЌИљОнШЋЕШШ§НЧаЮЕФаджЪЕУЕНOG=OAЃЌМДПЩЕУЕННсТлЃЎ
ЃЈ180ЁуЉЁЯEOFЃЉ=30ЁуЃЌгкЪЧЕУЕНЁЯAFO=ЁЯGFOЃЌЙ§OзїOGЁЭEFгкGЃЌИљОнШЋЕШШ§НЧаЮЕФаджЪЕУЕНOG=OAЃЌМДПЩЕУЕННсТлЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉжЄУїЃКЁпBCЪЧЁбOЕФжБОЖЃЌЁрЁЯBAC=90ЁуЃЌЁпЁЯABC=30ЁуЃЌЁрЁЯACB=60Ёу
ЁпOA=OCЃЌЁрЁЯAOC=60ЁуЃЌЁпAFЪЧЁбOЕФЧаЯпЃЌЁрЁЯOAF=90ЁуЃЌЁрЁЯAFC=30ЁуЃЌЁпDEЪЧЁбOЕФЧаЯпЃЌЁрЁЯDBC=90ЁуЃЌЁрЁЯD=ЁЯAFC=30ЃЌЁпЁЯDAE=ACF=120ЁуЃЌЁрЁїACFЁзЁїDAEЃЛ
ЃЈ2ЃЉЁпЁЯACO=ЁЯAFC+ЁЯCAF=30Ёу+ЁЯCAF=60ЁуЃЌЁрЁЯCAF=30ЁуЃЌЁрЁЯCAF=ЁЯAFCЃЌЁрAC=CFЃЌЁрOC=CFЃЌЁпSЁїAOC=![]() ЃЌЁрSЁїACF=
ЃЌЁрSЁїACF=![]() ЃЌЁпЁЯABC=ЁЯAFC=30ЁуЃЌЁрAB=AFЃЌЁпAB=
ЃЌЁпЁЯABC=ЁЯAFC=30ЁуЃЌЁрAB=AFЃЌЁпAB=![]() BDЃЌЁрAF=
BDЃЌЁрAF=![]() BDЃЌЁрЁЯBAE=ЁЯBEA=30ЁуЃЌЁрAB=BE=AFЃЌЁр
BDЃЌЁрЁЯBAE=ЁЯBEA=30ЁуЃЌЁрAB=BE=AFЃЌЁр![]() ЃЌЁпЁїACFЁзЁїDAEЃЌЁр
ЃЌЁпЁїACFЁзЁїDAEЃЌЁр![]() =
=![]() ЃЌЁрSЁїDAE=
ЃЌЁрSЁїDAE=![]() ЃЌЙ§AзїAHЁЭDEгкHЃЌЁрAH=
ЃЌЙ§AзїAHЁЭDEгкHЃЌЁрAH=![]() DH=
DH=![]() DEЃЌЁрSЁїADE=
DEЃЌЁрSЁїADE=![]() DEAH=
DEAH=![]() ЁС
ЁС![]()
![]() =
=![]() ЃЌЁрDE=
ЃЌЁрDE=![]() ЃЛ
ЃЛ
ЃЈ3ЃЉЁпЁЯEOF=ЁЯAOB=120ЁуЃЌЁрЁЯOEB=ЁЯAFOЃЌдкЁїAOFгыЁїBOEжаЃЌЁпЁЯOBE=ЁЯOAFЃЌЁЯOEB=ЁЯAFOЃЌOA=OBЃЌЁрЁїAOFЁеЁїBEOЃЌЁрOE=OFЃЌЁрЁЯOFG=![]() ЃЈ180ЁуЉЁЯEOFЃЉ=30ЁуЃЌЁрЁЯAFO=ЁЯGFOЃЌЙ§OзїOGЁЭEFгкGЃЌЁрЁЯOAF=ЁЯOGF=90ЁуЃЌдкЁїAOFгыЁїOGFжаЃЌЁпЁЯOAF=ЁЯOGFЃЌЁЯAFO=ЁЯGFOЃЌOF=OFЃЌЁрЁїAOFЁеЁїGOFЃЌЁрOG=OAЃЌЁрEFЪЧЁбOЕФЧаЯпЃЎ
ЃЈ180ЁуЉЁЯEOFЃЉ=30ЁуЃЌЁрЁЯAFO=ЁЯGFOЃЌЙ§OзїOGЁЭEFгкGЃЌЁрЁЯOAF=ЁЯOGF=90ЁуЃЌдкЁїAOFгыЁїOGFжаЃЌЁпЁЯOAF=ЁЯOGFЃЌЁЯAFO=ЁЯGFOЃЌOF=OFЃЌЁрЁїAOFЁеЁїGOFЃЌЁрOG=OAЃЌЁрEFЪЧЁбOЕФЧаЯпЃЎ
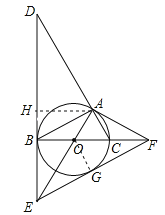
ЁОЬтаЭЁПНтД№Ьт
ЁОНсЪјЁП
25
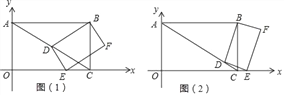
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌOЮЊдЕуЃЌЫФБпаЮABCOЪЧОиаЮЃЌЕуAЃЌCЕФзјБъЗжБ№ЪЧAЃЈ0ЃЌ2ЃЉКЭCЃЈ2![]() ЃЌ0ЃЉЃЌЕуDЪЧЖдНЧЯпACЩЯвЛЖЏЕуЃЈВЛгыAЃЌCжиКЯЃЉЃЌСЌНсBDЃЌзїDEЁЭDBЃЌНЛxжсгкЕуEЃЌвдЯпЖЮDEЃЌDBЮЊСкБпзїОиаЮBDEFЃЎ
ЃЌ0ЃЉЃЌЕуDЪЧЖдНЧЯпACЩЯвЛЖЏЕуЃЈВЛгыAЃЌCжиКЯЃЉЃЌСЌНсBDЃЌзїDEЁЭDBЃЌНЛxжсгкЕуEЃЌвдЯпЖЮDEЃЌDBЮЊСкБпзїОиаЮBDEFЃЎ
ЃЈ1ЃЉЬюПеЃКЕуBЕФзјБъЮЊЁЁ ЁЁЃЛ
ЃЈ2ЃЉЪЧЗёДцдкетбљЕФЕуDЃЌЪЙЕУЁїDECЪЧЕШбќШ§НЧаЮЃПШєДцдкЃЌЧыЧѓГіADЕФГЄЖШЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ3ЃЉЂйЧѓжЄЃК![]() ЃЛ
ЃЛ
ЂкЩшAD=xЃЌОиаЮBDEFЕФУцЛ§ЮЊyЃЌЧѓyЙигкxЕФКЏЪ§ЙиЯЕЪНЃЈПЩРћгУЂйЕФНсТлЃЉЃЌВЂЧѓГіyЕФзюаЁжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЪ§жсЩЯЕуAБэЪОЪ§aЃЌЕуBБэЪОЪ§bЃЌaЁЂbТњзу|aЉ20|+ЃЈb+10ЃЉ2ЃН0ЃЌOЪЧЪ§жсдЕуЃЌЕуQДгЕуBГіЗЂЃЌвдУПУы3ИіЕЅЮЛГЄЖШЕФЫйЖШбиЪ§жсе§ЗНЯђдШЫйдЫЖЏЃЌЩшдЫЖЏЪБМфЮЊtУыЃЎ
![]()
ЃЈ1ЃЉЕуAБэЪОЕФЪ§ЮЊЁЁ ЁЁЃЌЕуBБэЪОЕФЪ§ЮЊЁЁ ЁЁЃЎ
ЃЈ2ЃЉtЮЊКЮжЕЪБЃЌBQЃН2AQЃЎ
ЃЈ3ЃЉШєдкЕуQДгЕуBГіЗЂЕФЭЌЪБЃЌЕуPДгЕуOГіЗЂЃЌвдУПУы2ИіЕЅЮЛГЄЖШЕФЫйЖШвЛжБбиЪ§жсе§ЗНЯђдШЫйдЫЖЏЃЌЖјЕуQдЫЖЏЕНЕуAЪБЃЌСЂМДИФБфдЫЖЏЗНЯђЃЌбиЪ§жсЕФИКЗНЯђдЫЖЏЃЌЕНДяЕуBЪБЭЃжЙдЫЖЏЃЌдкЕуQЕФећИідЫЖЏЙ§ГЬжаЃЌЪЧЗёДцдкКЯЪЪЕФtжЕЃЌЪЙЕУPQЃН6ЃПШєДцдкЃЌЧѓГіЫљгаЗћКЯЬѕМўЕФtжЕЃЌШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
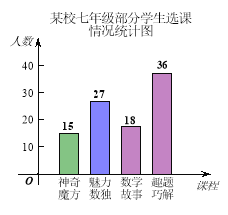
ЁОЬтФПЁПЃЈБОЬт8ЗжЃЉЮЊХрбјбЇЩњЪ§бЇбЇЯАаЫШЄЃЌФГаЃЦпФъМЖзМБИПЊЩшЁАЩёЦцФЇЗНЁБЁЂЁАїШСІЪ§ЖРЁБЁЂЁАЪ§бЇЙЪЪТЁБЁЂЁАШЄЬтЧЩНтЁБЫФУХбЁаоПЮЃЈУПЮЛбЇЩњБиаыЧвжЛбЁЦфжавЛУХЃЉЃЎ
ЃЈ1ЃЉбЇаЃЖдЦпФъМЖВПЗжбЇЩњНјаабЁПЮЕїВщЃЌЕУЕНШчЭМЫљЪОЕФЭГМЦЭМЃЌИљОнИУЭГМЦЭМЃЌЧыЙРМЦИУаЃЦпФъМЖ480УћбЇЩњбЁЁАЪ§бЇЙЪЪТЁБЕФШЫЪ§ЁЃ
ЃЈ2ЃЉбЇаЃНЋбЁЁАЪ§бЇЙЪЪТЁБЕФбЇЩњЗжГЩШЫЪ§ЯрЕШЕФAЃЌBЃЌCШ§ИіАрЃЌаЁДЯЁЂаЁЛлЖМбЁдёСЫЁАЪ§бЇЙЪЪТЁБЃЌвбжЊаЁДЯВЛдкAАрЃЌЧѓЫћКЭаЁЛлБЛЗжЕНЭЌвЛИіАрЕФИХТЪЃЎЃЈвЊЧѓСаБэЛђЛЪїзДЭМЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌОиаЮABCDЕФУцЛ§ЮЊ20cm2ЃЌЖдНЧЯпНЛгкЕуOЃЛвдABЁЂAOЮЊСкБпзіЦНааЫФБпаЮAOC1BЃЌЖдНЧЯпНЛгкЕуO1ЃЛвдABЁЂAO1ЮЊСкБпзіЦНааЫФБпаЮAO1C2BЃЛЁвРДЫРрЭЦЃЌдђЦНааЫФБпаЮAO4C5BЕФУцЛ§ЮЊЃЈ ЃЉ

A. ![]() cm2 B.
cm2 B. ![]() cm2 C.
cm2 C. ![]() cm2 D.
cm2 D. ![]() cm2
cm2
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
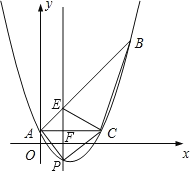
ЁОЬтФПЁПШчЭМ,вбжЊХзЮяЯпy=![]() x2+bx+cОЙ§ЁїABCЕФШ§ИіЖЅЕу,ЦфжаЕуA(0,1),B(9,10),ACЁЮxжсЃЌЕуPЪЧжБЯпACЯТЗНХзЮяЯпЩЯЕФЖЏЕуЁЃ
x2+bx+cОЙ§ЁїABCЕФШ§ИіЖЅЕу,ЦфжаЕуA(0,1),B(9,10),ACЁЮxжсЃЌЕуPЪЧжБЯпACЯТЗНХзЮяЯпЩЯЕФЖЏЕуЁЃ
(1)ЧѓХзЮяЯпЕФНтЮіЪНЃЛ
(2)Й§ЕуPЧвгыyжсЦНааЕФжБЯпlгыжБЯпABЁЂACЗжБ№НЛгкЕуE.FЃЌЕБЫФБпаЮAECPЕФУцЛ§зюДѓЪБЃЌЧѓЕуPЕФзјБъКЭЫФБпаЮAECPЕФзюДѓУцЛ§ЃЛ
(3)ЕБЕуPЮЊХзЮяЯпЕФЖЅЕуЪБЃЌдкжБЯпACЩЯЪЧЗёДцдкЕуQЃЌЪЙЕУвдC.PЁЂQЮЊЖЅЕуЕФШ§НЧаЮгыЁїABCЯрЫЦ?ШєДцдкЃЌЧѓГіЕуQЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЁЃ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com