
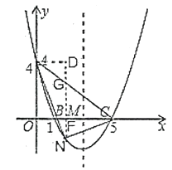
【题目】如图,在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于
轴交于![]() 两点,其对称轴与
两点,其对称轴与![]() 轴交于点
轴交于点![]() .
.
(1)求抛物线的解析式和对称轴;
(2)在抛物线的对称轴上是否存在一点![]() ,使
,使![]() 的周长最小?若存在,请求出点
的周长最小?若存在,请求出点![]() 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;
(3)连接![]() ,在直线
,在直线![]() 的下方的抛物线上,是否存在一点
的下方的抛物线上,是否存在一点![]() ,使
,使![]() 的面积最大?若存在,请求出点
的面积最大?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
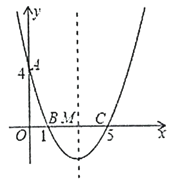
【答案】(1)![]() ,抛物线的对称轴是
,抛物线的对称轴是![]() ;(2)
;(2)![]() 点坐标为
点坐标为![]() .理由见解析;(3)在直线
.理由见解析;(3)在直线![]() 的下方的抛物线上存在点
的下方的抛物线上存在点![]() ,使
,使![]() 面积最大.点
面积最大.点![]() 的坐标为
的坐标为![]() .
.
【解析】
(1)根据点B,C的坐标,利用待定系数法可求出抛物线的解析式,再利用二次函数的性质可求出抛物线的对称轴;
(2)连接![]() 交对称轴于点
交对称轴于点![]() ,此时
,此时![]() 的周长最小,利用二次函数图象上点的坐标特征可求出点
的周长最小,利用二次函数图象上点的坐标特征可求出点![]() 的坐标,由点
的坐标,由点![]() ,B的坐标,利用待定系数法可求出直线AC的解析式,再利用一次函数图象上点的坐标特征可求出点P的坐标;
,B的坐标,利用待定系数法可求出直线AC的解析式,再利用一次函数图象上点的坐标特征可求出点P的坐标;
(3)过点N作NE∥y轴交AC于点E,交x轴于点F,过点A作AD⊥NE于点D,设点N的坐标为(t,![]() t2-
t2-![]() t+4)(0<t<5),则点E的坐标为(t,-
t+4)(0<t<5),则点E的坐标为(t,-![]() t+4),进而可得出NE的长,由三角形的面积公式结合S△CAN=S△NAE+S△NCE可得出S△CAN关于t的函数关系式,再利用二次函数的性质即可解决最值问题.
t+4),进而可得出NE的长,由三角形的面积公式结合S△CAN=S△NAE+S△NCE可得出S△CAN关于t的函数关系式,再利用二次函数的性质即可解决最值问题.
(1)根据已知条件可设抛物线的解析式为![]() ,
,
∴![]() ,
,
∴抛物线的对称轴是![]() ;
;
(2)![]() 点坐标为
点坐标为![]() .
.
理由如下:
∵点![]() (0,4),抛物线的对称轴是
(0,4),抛物线的对称轴是![]() ,
,
∴点![]() 关于对称轴的对称点
关于对称轴的对称点![]() 的坐标为(6,4),
的坐标为(6,4),
如图1,连接![]() 交对称轴于点
交对称轴于点![]() ,连接
,连接![]() ,此时
,此时![]() 的周长最小.
的周长最小.
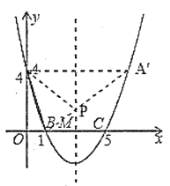
设直线![]() 的解析式为
的解析式为![]() ,
,
把![]() (6,4),
(6,4),![]() (1,0)代入得
(1,0)代入得![]() ,
,
解得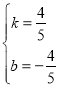 ,
,
∴![]() ,
,
∵点![]() 的横坐标为3,
的横坐标为3,
∴点![]() 的纵坐标为
的纵坐标为![]() ,
,
∴所求点![]() 的坐标为
的坐标为![]() .
.
(3)在直线![]() 的下方的抛物线上存在点
的下方的抛物线上存在点![]() ,使
,使![]() 面积最大.
面积最大.
设![]() 点的横坐标为
点的横坐标为![]() ,此时点
,此时点![]() ,
,
如图2,过点![]() 作
作![]() 轴交
轴交![]() 于
于![]() ;作
;作![]() 于点
于点![]() ,
,
由点![]() (0,4)和点
(0,4)和点![]() (5,0)得直线
(5,0)得直线![]() 的解析式为
的解析式为![]() ,
,
把![]() 代入得
代入得![]() ,则
,则![]() ,
,
此时![]() ,
,
∵![]() ,
,
∴![]()
![]() ,
,
∴当![]() 时,
时,![]() 面积的最大值为
面积的最大值为![]() ,
,
由![]() 得
得![]() ,
,
∴点![]() 的坐标为
的坐标为![]() .
.


 初中暑期衔接系列答案
初中暑期衔接系列答案科目:初中数学 来源: 题型:
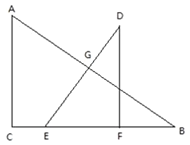
【题目】如图,在![]() 中,
中,![]() ,
,![]() cm,
cm,![]() cm,在
cm,在![]() 中,
中,![]() ,
,![]() cm,
cm,![]() cm.EF在BC上,保持
cm.EF在BC上,保持![]() 不动,并将
不动,并将![]() 以1cm/s的速度向点C运动,移动开始前点F与点B重合,当点E与点C重合时,
以1cm/s的速度向点C运动,移动开始前点F与点B重合,当点E与点C重合时,![]() 停止移动.边DE与AB相交于点G,连接FG,设移动时间为t(s).
停止移动.边DE与AB相交于点G,连接FG,设移动时间为t(s).
(1)![]() 从移动开始到停止,所用时间为________s;
从移动开始到停止,所用时间为________s;
(2)当DE平分AB时,求t的值;
(3)当![]() 为等腰三角形时,求t的值.
为等腰三角形时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公园的门票价格如下表:
购票人数 | 1-50人 | 51-100人 | 100人以上 |
每人门票数 | 13元 | 11元 | 9元 |
实验学校初二(1)、二(2)两个班的学生共104人去公园游玩,其中二(1)班的人数不到50人,二(2)班的人数有50多人,经估算,如果两个班都以班为单位分别购票,则一共应付1240元,如果两班联合起来,作为一个团体购票,则可节省不少钱,你能否求出两个班共有多少名学生联合起来购票能省多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,AC是弦,直线EF经过点C,AD⊥EF于点D,∠DAC=∠BAC.
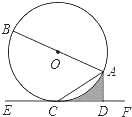
(1)求证:EF是⊙O的切线;
(2)若⊙O的半径为2,∠ACD=30°,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
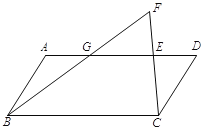
【题目】如图,□ABCD中,∠ABC为锐角,AB<BC,点E是AD上的一点,延长CE到F,连接BF交AD于点G, 使∠FBC=∠DCE.
⑴ 求证:∠D=∠F;
⑵ 在直线AD找一点P,使以点B、P、C为顶点的三角形与以点C、D、P为顶点的三角形相似.(在原图中标出准确P点的位置,必要时用直尺和圆规作出P点,保留作图的痕迹,不写作法)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点C在线段AB上,AC=2BC,点D、E在直线AB上,点D在点E的左侧
(1)若AB=18,DE=8,线段DE在线段AB上移动
①如图1,当E为BC中点时,求AD的长;
②点F(异于A,B,C点)在线段AB上,AF=3AD,CE+EF=3,求AD的长;
(2)若AB=2DE,线段DE在直线AB上移动,且满足关系式![]() ,则
,则![]() ______.
______.
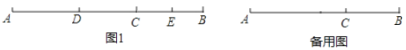
查看答案和解析>>
科目:初中数学 来源: 题型:
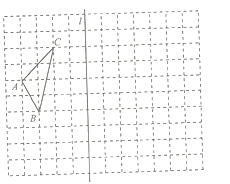
【题目】如图,在![]() 的正方形网格中,
的正方形网格中,![]() 是格点三角形,点
是格点三角形,点![]() 的坐标分别为
的坐标分别为![]() ,
,![]() .
.
(1)在图中画出相应的平面直角坐标系;
(2)画出![]() 关于直线
关于直线![]() 对称的
对称的![]() ,并标出点
,并标出点![]() 的坐标;
的坐标;
(3)若点![]() 在
在![]() 内,其关于直线
内,其关于直线![]() 的对称点是
的对称点是![]() ,则
,则![]() 的坐标是 .
的坐标是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一个边长为a的正方形分成9个完全相同的小正方形,把最中间的一个小正方形涂成白色(图①),再对其他8个小正方形作同样的分割(分成9个完全相同的小正方形,把最中间的一个小正方形涂成白色(图②),继续同样的方法分割图形(图③),…得到一些既复杂又漂亮的图形,它的每一部分放大,都和整体一模一样,它是波兰数学家谢尔宾斯基构造的,也被称为“谢尔宾斯基地毯”.求:
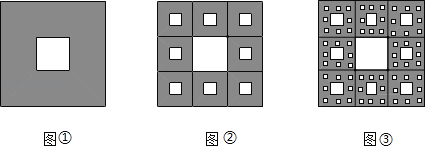
(1)图③中最新的一个最小正方形的边长;
(2)图③中所有涂黑部分的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com