
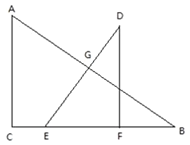
【题目】如图,在![]() 中,
中,![]() ,
,![]() cm,
cm,![]() cm,在
cm,在![]() 中,
中,![]() ,
,![]() cm,
cm,![]() cm.EF在BC上,保持
cm.EF在BC上,保持![]() 不动,并将
不动,并将![]() 以1cm/s的速度向点C运动,移动开始前点F与点B重合,当点E与点C重合时,
以1cm/s的速度向点C运动,移动开始前点F与点B重合,当点E与点C重合时,![]() 停止移动.边DE与AB相交于点G,连接FG,设移动时间为t(s).
停止移动.边DE与AB相交于点G,连接FG,设移动时间为t(s).
(1)![]() 从移动开始到停止,所用时间为________s;
从移动开始到停止,所用时间为________s;
(2)当DE平分AB时,求t的值;
(3)当![]() 为等腰三角形时,求t的值.
为等腰三角形时,求t的值.
【答案】(1)6;(2)![]() ;(3)t=
;(3)t=![]() ,4,6
,4,6
【解析】
(1)直接用行程问题的数量关系计算可得;
(2)连接AE,证明DE是AB的垂直平分线,然后Rt![]() 中,由勾股定理得:
中,由勾股定理得:
![]() 即
即![]() ,解方程即可得出t的值;
,解方程即可得出t的值;
(3)分三种情况讨论等腰三角形的情况,利用平行线分线段成比例定理和勾股定理可得列出方程,求出HG的值并进一步得到BF的值,从而得出t的值。
解:(1)如图1
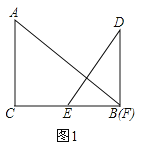
∵BC=12cm,EF=6cm,
∴EC=12-6=6cm,
6÷1=6s
∴![]() 从移动开始到停止,所用时间为6s;
从移动开始到停止,所用时间为6s;
故答案为:6
(2)如图2,连接AE
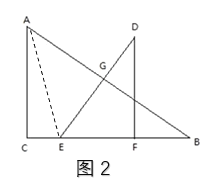
∵EF:DF=AC:BC=3:4,![]()
∴![]() ∽
∽![]() ,
,
∴∠D=∠B
∴DG⊥AB,
∵DG平分AB,
∴AE=BE=t+6
CE=6-t
在Rt![]() 中,由勾股定理得:
中,由勾股定理得:
![]() 即
即![]()
解得t=![]() s
s
(3)如图3,连接GF, 过点G作GH⊥BC于点H,
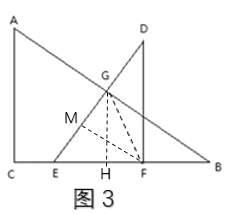
由勾股定理得ED=10
![]() 为等腰三角形,分三种情况讨论:
为等腰三角形,分三种情况讨论:
①当EF=EG=6时,
∵![]() ,即
,即![]()
解得GH=4.8
由勾股定理得EH=3.6
∵![]() ,即
,即![]()
解得BH=6.4
∴BE=6.4+3.6=10
∴BF=10-6=4
∴t=4
②当GF=EF=6时,过点F作FM⊥GE于点M,
设ME=3x,则MF=4x, 由勾股定理得:
![]()
解得x=1.2
∴GE=6x=7.2,
设EH=3y,则GH=4y,, 由勾股定理得:
![]()
解得:y=1.44
∴EH=4.32,则GH=5.76
![]()
解得BH=7.68
则BE=7.68+4.32=12
BF=12-6=6
∴t=6
③当GE=GF时,
EH=FH=3,则GH=4
![]()
解得BH=![]()
则BF=BH-FH=![]()
∴t=![]()
综上所述,当t=![]() ,4,6时,
,4,6时,![]() 为等腰三角形。
为等腰三角形。


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:
【题目】如图在直角坐标平面内,抛物线![]() 与
与![]() 轴交于点A,与x轴分别交于点B(-1,0)、点C(3,0),点D是抛物线的顶点.
轴交于点A,与x轴分别交于点B(-1,0)、点C(3,0),点D是抛物线的顶点.
(1)求抛物线的表达式及顶点D的坐标;
(2)连接AD、DC,求![]() 的面积;
的面积;
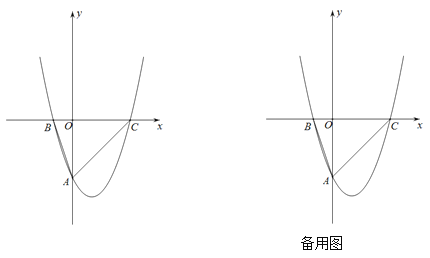
(3)点P在直线DC上,联结OP,若以O、P、C为顶点的三角形与△ABC相似,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车从A城出发前往B城.在整个行程中,汽车离开A城的距离y与时刻t的对应关系如图所示.
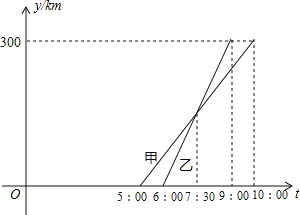
(1)A,B两城相距 km;
(2)哪辆车先出发?哪辆车先到B城?
(3)甲车的平均速度为 km/h,乙车的平均速度为 km/s?
(4)你还能从图中得到哪些信息?
查看答案和解析>>
科目:初中数学 来源: 题型:
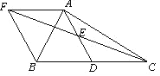
【题目】如图,在![]() 中,D是BC的中点,E是AD的中点,过点A作
中,D是BC的中点,E是AD的中点,过点A作![]() ,AF与CE的延长线相交于点F,连接BF.
,AF与CE的延长线相交于点F,连接BF.
(1)求证:四边形AFBD是平行四边形;
(2)①若四边形AFBD是矩形,则![]() 必须满足条件_________;
必须满足条件_________;
②若四边形AFBD是菱形,则![]() 必须满足条件_________.
必须满足条件_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校开运动会,要买一批笔记本和圆珠笔作为奖品,笔记本要买50本,圆珠笔要买若干支.张老师去了两家文具店,笔记本和圆珠笔的零售价分别为3元和2元,但甲文具店的营业员说:“如果笔记本按零售价,那么圆珠笔可按零售价的8折优惠.”乙文具店的营业员说:“笔记本和圆珠笔可按9折优惠.”
(1)若要购买的圆珠笔为![]() 支,用含
支,用含![]() 的式子表示甲、乙两个店的收费;
的式子表示甲、乙两个店的收费;
(2)若学校要买100支圆珠笔作为奖品,你认为张老师去哪家文具店较合算?可节省多少钱?
(3)若买圆珠笔![]() 支时,选择甲文具店较合算,求此时可节省多少钱?
支时,选择甲文具店较合算,求此时可节省多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下图是某同学在沙滩上用石子摆成的小房子,请根据图中的信息完成下列的问题:

(1)填写下表:
图形编号 | ① | ② | ③ | ④ | …… |
图中石子的总数 | …… |
(2)第30个图形需要用 颗石子;
(3)如果继续摆放下去,那么第![]() 个图案要用 颗石子;
个图案要用 颗石子;
(4)该同学准备用300颗石子来摆放第![]() 个图案,摆放成完整的图案后,第
个图案,摆放成完整的图案后,第![]() 个图案 能否刚好用完这300颗石子?如果可以,求出
个图案 能否刚好用完这300颗石子?如果可以,求出![]() 的值,如果不能,求出
的值,如果不能,求出![]() 的最大值以及至少还剩余多少颗石子.
的最大值以及至少还剩余多少颗石子.
查看答案和解析>>
科目:初中数学 来源: 题型:
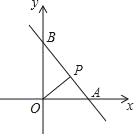
【题目】如图,直线y=3﹣2x与x轴,y轴分别相交于点A,B,点P(x,y)是线段AB上的任意一点,并设△OAP的面积为S.
(1)S与x的函数解析式,求自变量x的取值范围.
(2)如果△OAP的面积大于1,求自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
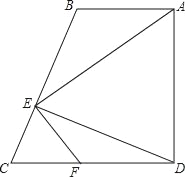
【题目】如图,在四边形ABCD中,AB∥CD,∠ADC=90°,DE⊥BC于E,连AE,FE⊥AE交CD于点F.
(1)求证:△AED∽△FEC;
(2)若AB=2![]() ,求DF的值;
,求DF的值;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com