
【题目】某学校开运动会,要买一批笔记本和圆珠笔作为奖品,笔记本要买50本,圆珠笔要买若干支.张老师去了两家文具店,笔记本和圆珠笔的零售价分别为3元和2元,但甲文具店的营业员说:“如果笔记本按零售价,那么圆珠笔可按零售价的8折优惠.”乙文具店的营业员说:“笔记本和圆珠笔可按9折优惠.”
(1)若要购买的圆珠笔为![]() 支,用含
支,用含![]() 的式子表示甲、乙两个店的收费;
的式子表示甲、乙两个店的收费;
(2)若学校要买100支圆珠笔作为奖品,你认为张老师去哪家文具店较合算?可节省多少钱?
(3)若买圆珠笔![]() 支时,选择甲文具店较合算,求此时可节省多少钱?
支时,选择甲文具店较合算,求此时可节省多少钱?
【答案】(1)1.6x+150,1.8x+135;(2)甲,5元;(3)(0.2y-15)元
【解析】
(1)根据题意可以分别列出甲、乙两文具店的收费;
(2)将x=80代入(1)中甲乙收费的式子中,然后进行比较即可解答本题;
(3)用乙的收费减去甲的收费即可得到在甲文具店可以省多少钱.
解:(1)由题意可得,
甲文具店的收费为:50×3+2x×0.8=1.6x+150,
乙文具店的收费为:(50×3+2x)×0.9=1.8x+135,
即甲文具店的收费为1.6x+150,乙文具店的收费为1.8x+135;
(2)当x=100时,甲文具店收费为:1.6×100+150=310(元),乙文具店收费为:1.8×100+135=315(元),
∵315>310,315-310=5,
∴学校要买100支圆珠笔作为奖品,我认为张老师应取甲文具店较合算,可节省5元;
(3)(1.8y+135)-(1.6y+150)
=1.8y+135-1.6y-150
=0.2y-15,
即要买圆珠笔y支时,选择甲文具店较合算,此时节省(0.2y-15)元.


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:初中数学 来源: 题型:
【题目】正方形ABCD,CEFG按如图放置,点B,C,E在同一条直线上,点P在BC边上,PA=PF,且∠APF=90°,连接AF交CD于点M,有下列结论:①EC=BP;②AP=AM;③∠BAP=∠GFP;④AB2+CE2=![]() AF2;⑤S正方形ABCD+S正方形CEFG=2S△APF.其中正确的是( )
AF2;⑤S正方形ABCD+S正方形CEFG=2S△APF.其中正确的是( )
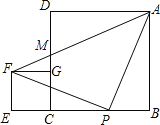
A. ①②③ B. ①③④ C. ①②④⑤ D. ①③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
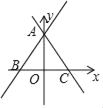
【题目】如图,直线y=![]() x+
x+![]() 与x轴相交于点B,与y轴相交于点A.
与x轴相交于点B,与y轴相交于点A.
(1)求∠ABO的度数;
(2)过点A的直线l交x轴的正半轴于点C,且AB=AC,求直线的函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人参加某体育项目训练,为了便于研究,把最后5次的训练成绩分别用实线和虚线连接起来,如图,下面的结论错误的是( )

A. 乙的第2次成绩与第5次成绩相同
B. 第3次测试,甲的成绩与乙的成绩相同
C. 第4次测试,甲的成绩比乙的成绩多2分
D. 在5次测试中,甲的成绩都比乙的成绩高
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() cm,
cm,![]() cm,在
cm,在![]() 中,
中,![]() ,
,![]() cm,
cm,![]() cm.EF在BC上,保持
cm.EF在BC上,保持![]() 不动,并将
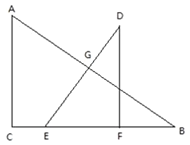
不动,并将![]() 以1cm/s的速度向点C运动,移动开始前点F与点B重合,当点E与点C重合时,
以1cm/s的速度向点C运动,移动开始前点F与点B重合,当点E与点C重合时,![]() 停止移动.边DE与AB相交于点G,连接FG,设移动时间为t(s).
停止移动.边DE与AB相交于点G,连接FG,设移动时间为t(s).
(1)![]() 从移动开始到停止,所用时间为________s;
从移动开始到停止,所用时间为________s;
(2)当DE平分AB时,求t的值;
(3)当![]() 为等腰三角形时,求t的值.
为等腰三角形时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+3(a≠0)经过点A(﹣1,0),B(![]() ,0),且与y轴相交于点C.
,0),且与y轴相交于点C.
(1)求这条抛物线的表达式;
(2)求∠ACB的度数;
(3)设点D是所求抛物线第一象限上一点,且在对称轴的右侧,点E在线段AC上,且DE⊥AC,当△DCE与△AOC相似时,求点D的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
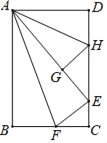
【题目】在数学拓展课《折叠矩形纸片》上,小林折叠矩形纸片ABCD进行如下操作:①把△ABF翻折,点B落在CD边上的点E处,折痕AF交BC边于点F;②把△ADH翻折,点D落在AE边长的点G处,折痕AH交CD边于点H.若AD=6,AB=10,则![]() 的值是( )
的值是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为创建“国家园林城市”,某校举行了以“爱我黄石”为主题的图片制作比赛,评委会对200名同学的参赛作品打分发现,参赛者的成绩x均满足50≤x<100,并制作了频数分布直方图,如图.
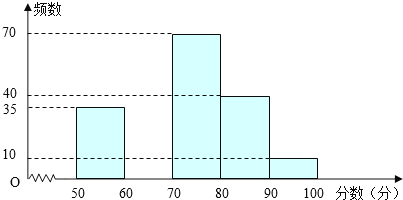
根据以上信息,解答下列问题:
(1)请补全频数分布直方图;
(2)若依据成绩,采取分层抽样的方法,从参赛同学中抽40人参加图片制作比赛总结大会,则从成绩80≤x<90的选手中应抽多少人?
(3)比赛共设一、二、三等奖,若只有25%的参赛同学能拿到一等奖,则一等奖的分数线是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
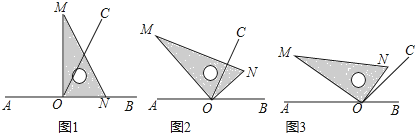
【题目】点O为直线AB上一点,过点O作射线OC,使∠BOC=65°,将一直角三角板的直角顶点放在点O处.
(1)如图①,将三角板MON的一边ON与射线OB重合时,则∠MOC= ;
(2)如图②,将三角板MON绕点O逆时针旋转一定角度,此时OC是∠MOB的角平分线,求旋转角∠BON和∠CON的度数;
(3)将三角板MON绕点O逆时针旋转至图③时,∠NOC=![]() ∠AOM,求∠NOB的度数.
∠AOM,求∠NOB的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com