
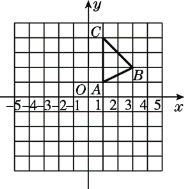
【题目】在平面直角坐标系中,△ABC的三个顶点坐标分别为:A(1,1),B(3,2),C(1,4).
(1)将△ABC先向下平移4个单位,再向右平移1个单位,画出第二次平移后的△A1B1C1.若将△A1B1C1看成是△ABC经过一次平移得到的,则平移距离是________.
(2)以原点为对称中心,画出与△ABC成中心对称的△A2B2C2.
科目:初中数学 来源: 题型:
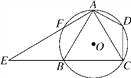
【题目】如图,已知四边形ABCD内接于⊙O,A是![]() 的中点,AE⊥AC于A,与⊙O及CB的延长线交于点F,E,且
的中点,AE⊥AC于A,与⊙O及CB的延长线交于点F,E,且![]() .
.
(1)求证:△ADC∽△EBA;
(2)如果AB=8,CD=5,求tan∠CAD的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
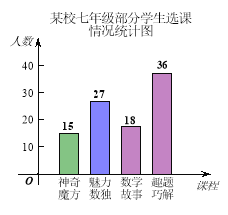
【题目】(本题8分)为培养学生数学学习兴趣,某校七年级准备开设“神奇魔方”、“魅力数独”、“数学故事”、“趣题巧解”四门选修课(每位学生必须且只选其中一门).
(1)学校对七年级部分学生进行选课调查,得到如图所示的统计图,根据该统计图,请估计该校七年级480名学生选“数学故事”的人数。
(2)学校将选“数学故事”的学生分成人数相等的A,B,C三个班,小聪、小慧都选择了“数学故事”,已知小聪不在A班,求他和小慧被分到同一个班的概率.(要求列表或画树状图)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的面积为20cm2,对角线交于点O;以AB、AO为邻边做平行四边形AOC1B,对角线交于点O1;以AB、AO1为邻边做平行四边形AO1C2B;…依此类推,则平行四边形AO4C5B的面积为( )

A. ![]() cm2 B.
cm2 B. ![]() cm2 C.
cm2 C. ![]() cm2 D.
cm2 D. ![]() cm2
cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】瞳瞳做一道数学题:求代数式![]() 当x=-1时的值,由于瞳瞳粗心把式子中的某一项前的“+”号错误地看成了“—”号,算出代数式的值是-11,那么瞳瞳看错的是 次项前的符号,写出x=-1和x=1时代数式的值.
当x=-1时的值,由于瞳瞳粗心把式子中的某一项前的“+”号错误地看成了“—”号,算出代数式的值是-11,那么瞳瞳看错的是 次项前的符号,写出x=-1和x=1时代数式的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某校为了创建书香校园,去年购进一批图书.经了解,科普书的单价比文学书的单价多4元,用12000元购进的科普书与用8000元购进的文学书本数相等.
(1)文学书和科普书的单价各多少钱?
(2)今年文学书和科普书的单价和去年相比保持不变,该校打算用10000元再购进一批文学书和科普书,问购进文学书550本后至多还能购进多少本科普书?
查看答案和解析>>
科目:初中数学 来源: 题型:
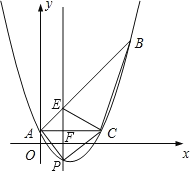
【题目】如图,已知抛物线y=![]() x2+bx+c经过△ABC的三个顶点,其中点A(0,1),B(9,10),AC∥x轴,点P是直线AC下方抛物线上的动点。
x2+bx+c经过△ABC的三个顶点,其中点A(0,1),B(9,10),AC∥x轴,点P是直线AC下方抛物线上的动点。
(1)求抛物线的解析式;
(2)过点P且与y轴平行的直线l与直线AB、AC分别交于点E.F,当四边形AECP的面积最大时,求点P的坐标和四边形AECP的最大面积;
(3)当点P为抛物线的顶点时,在直线AC上是否存在点Q,使得以C.P、Q为顶点的三角形与△ABC相似?若存在,求出点Q的坐标;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(知识背景)
据我国古代《周髀算经》记载,公元前1120年商高对周公说,将一根直尺折成一个直角,两端连接得到一个直角三角形,如果勾是3,股是4,那么弦就等于5,后人概括为“勾三、股四、弦五”.像3、4、5这样为三边长能构成直角三角形的三个正整数,称为勾股数.
(应用举例)
观察3,4,5;5,12,13;7,24,25;…
可以发现这些勾股数的勾都是奇数,且从3起就没有间断过,并且
勾为3时,股![]() ,弦
,弦![]() ;
;
勾为5时,股![]() ,弦
,弦![]() ;
;
请仿照上面两组样例,用发现的规律填空:
(1)如果勾为7,则股24= 弦25=
(2)如果勾用![]() (
(![]() ,且
,且![]() 为奇数)表示时,请用含有
为奇数)表示时,请用含有![]() 的式子表示股和弦,则股= ,弦= .
的式子表示股和弦,则股= ,弦= .
(解决问题)
观察4,3,5;6,8,10;8,15,17;…根据应用举例获得的经验进行填空:
(3)如果![]() 是符合同样规律的一组勾股数,
是符合同样规律的一组勾股数,![]() (
(![]() 表示大于1的整数),则
表示大于1的整数),则![]() ,
,![]() ,这就是古希腊的哲学家柏拉图提出的构造勾股数组的公式.
,这就是古希腊的哲学家柏拉图提出的构造勾股数组的公式.
(4)请你利用柏拉图公式,补全下面两组勾股数(数据从小到大排列)第一组: 、24、 :第二组: 、 、37.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com