
【题目】(知识背景)
据我国古代《周髀算经》记载,公元前1120年商高对周公说,将一根直尺折成一个直角,两端连接得到一个直角三角形,如果勾是3,股是4,那么弦就等于5,后人概括为“勾三、股四、弦五”.像3、4、5这样为三边长能构成直角三角形的三个正整数,称为勾股数.
(应用举例)
观察3,4,5;5,12,13;7,24,25;…
可以发现这些勾股数的勾都是奇数,且从3起就没有间断过,并且
勾为3时,股![]() ,弦
,弦![]() ;
;
勾为5时,股![]() ,弦
,弦![]() ;
;
请仿照上面两组样例,用发现的规律填空:
(1)如果勾为7,则股24= 弦25=
(2)如果勾用![]() (
(![]() ,且
,且![]() 为奇数)表示时,请用含有
为奇数)表示时,请用含有![]() 的式子表示股和弦,则股= ,弦= .
的式子表示股和弦,则股= ,弦= .
(解决问题)
观察4,3,5;6,8,10;8,15,17;…根据应用举例获得的经验进行填空:
(3)如果![]() 是符合同样规律的一组勾股数,
是符合同样规律的一组勾股数,![]() (
(![]() 表示大于1的整数),则
表示大于1的整数),则![]() ,
,![]() ,这就是古希腊的哲学家柏拉图提出的构造勾股数组的公式.
,这就是古希腊的哲学家柏拉图提出的构造勾股数组的公式.
(4)请你利用柏拉图公式,补全下面两组勾股数(数据从小到大排列)第一组: 、24、 :第二组: 、 、37.
【答案】(1)![]() ;
;![]() ;(2)
;(2)![]() ;
;![]() ;(3)
;(3)![]() ;
;![]() ;(4)10;26; 12;35;
;(4)10;26; 12;35;
【解析】
(1)依据规律可得,如果勾为7,则股24=![]() ,
,
弦25=![]() ;
;
(2)如果勾用n(n≥3,且n为奇数)表示时,则股=![]() ,
,
弦=![]() ;
;
(3)根据规律可得,如果a,b,c是符合同样规律的一组勾股数,a=2m(m表示大于1的整数),则b=m2-1,c=m2+1;
(4)依据柏拉图公式,若m2-1=24,则m=5,2m=10,m2+1=26;若m2+1=37,则m=6,2m=12,m2-1=35.
解:(1)依据规律可得,如果勾为7,则股24=![]() ,
,
弦25=![]() ;
;
故答案为:![]() ;
;![]() ;
;
(2)如果勾用n(n≥3,且n为奇数)表示时,则股=![]() ,
,
弦=![]() ;
;
故答案为:![]() ;
;![]() ;
;
(3)根据规律可得,如果a,b,c是符合同样规律的一组勾股数,a=2m(m表示大于1的整数),则b=m2-1,c=m2+1;
故答案为:m2-1,m2+1;
(4)依据柏拉图公式,
若m2-1=24,则m=5,2m=10,m2+1=26;
若m2+1=37,则m=6,2m=12,m2-1=35;
故答案为:10、26;12、35.


科目:初中数学 来源: 题型:
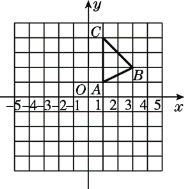
【题目】在平面直角坐标系中,△ABC的三个顶点坐标分别为:A(1,1),B(3,2),C(1,4).
(1)将△ABC先向下平移4个单位,再向右平移1个单位,画出第二次平移后的△A1B1C1.若将△A1B1C1看成是△ABC经过一次平移得到的,则平移距离是________.
(2)以原点为对称中心,画出与△ABC成中心对称的△A2B2C2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】让我们轻松一下,做一个数字游戏。第一步:取一个自然数n1=5,计算n12+1得a1;第二步:算出a1的各位数字之和得n2,计算n22+1得a2;第三步,算出a2的各位数字之和得n3,计算n32+1得a3;…………以此类推,则a2019=__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有3张纸牌,分別是红桃3、红桃4和黑桃5(简称红3,红4,黑5).把牌洗匀后甲先抽取一张,记下花色和数字后将牌放回,洗匀后乙再抽取一张.
(1)两次抽得纸牌均为红桃的概率;(请用“画树状图”或“列表”等方法写出分析过程)
(2)甲、乙两人做游戏,现有两种方案.A方案:若两次抽得花色相同则甲胜,否则乙胜.B方案:若两次抽得纸牌的数字和为奇数则甲胜,否则乙胜.请问甲选择哪种方案胜率更高?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级学生小丽、小强和小红到某超市参加了社会实践活动,在活动中他们参与了某种水果的销售工作.已知该水果的进价为8元/千克,下面是他们在活动结束后的对话.
小丽:如果以10元/千克的价格销售,那么每天可售出300千克.
小强:如果每千克的利润为3元,那么每天可售出250千克.
小红:如果以13元/千克的价格销售,那么每天可获取利润750元.
【利润=(销售价-进价)![]() 销售量】
销售量】
(1)请根据他们的对话填写下表:
销售单价x(元/kg) | 10 | 11 | 13 |
销售量y(kg) |
(2)请你根据表格中的信息判断每天的销售量y(千克)与销售单价x(元)之间存在怎样的函数关系.并求y(千克)与x(元)(x>0)的函数关系式;
(3)设该超市销售这种水果每天获取的利润为W元,求W与x的函数关系式.当销售单价为何值时,每天可获得的利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某种产品展开图,高为3cm.
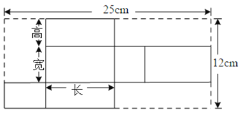
(1)求这个产品的体积.
(2)请为厂家设计一种包装纸箱,使每箱能装5件这种产品,要求没有空隙且要使该纸箱所用材料尽可能少(纸的厚度不计,纸箱的表面积尽可能小),求此长方体的表面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小强在某超市同时购买A,B两种商品共三次,仅有第一次超市将A,B两种商品同时按![]() 折价格出售,其余两次均按标价出售. 小强三次购买A,B商品的数量和费用如下表所示:
折价格出售,其余两次均按标价出售. 小强三次购买A,B商品的数量和费用如下表所示:
A商品的数量(个) | B商品的数量(个) | 购买总费用(元) | |
第一次购买 | 8 | 6 | 930 |
第二次购买 | 6 | 5 | 980 |
第三次购买 | 3 | 8 | 1040 |
(1)求 A,B商品的标价;
(2)求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为进一步推进青少年阳光工程,树立“每天锻炼一小时,快乐学习一整天”的指导思想,郑州市教育局部署了校园阳光大课间活动郑州市某中学体育组为了了解七年级学生的体能情况,组织七年级学生进行了1分钟跳绳测试,并将测试成绩(即1分钟跳绳的个数)分段后给出相应等级,具体为:测试成绩在60~90范围内的记为D级,90~120范围内的记为C级,120~150范围内的记为B级,150~180及以上范围内的记为A级,并绘出了测试成绩频数分布直方图及扇形统计图,其中在扇形统计图中A级对应的圆心角为54°,
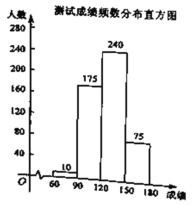

请根据图中的信息解答下列问题:
(1)在扇形统计图中,A级所占百分比为 %;
(2)在扇形统计图中,求D级对应的圆心角的度数;
(3)请结合统计图给出合理的运动建议.(至少写出两条)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com