【题目】在美化校园的活动中，某兴趣小组想借助如图所示的直角墙角(两边足够长)，用32m长的篱笆围成一个矩形花园ABCD(篱笆只围AB，BC两边)，设AB＝xm．
(1)若花园的面积为252m2，求x的值；
(2)若在P处有一棵树与墙CD，AD的距离分别是17m和6m，要将这棵树围在花园内(含边界，不考虑树的粗细)，求花园面积S的最大值．
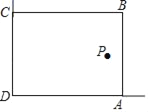
【答案】（1）18m或14m；（2）花园面积的最大值是255平方米．
【解析】
（1）根据AB=x米可知BC=（32-x）米，再根据矩形的面积公式即可得出结论；
（2）根据P处有一棵树与墙CD、AD的距离分别是18米和8米求出x的取值范围，再根据（1）中的函数关系式即可得出结论．
解：（1）设AB=x米，可知BC=（32-x）米，根据题意得：x（32-x）=252．
解这个方程得：x1=18，x2=14，
答：x的长度18m或14m．
（2）设周围的矩形面积为S，
则S=x（32-x）=-（x-16）2+256．
∵在P处有一棵树与墙CD，AD的距离是17m和6米，
∴6≤x≤15．
∴当x=15时，S最大= -（15-16）2+256=255（平方米）．
答：花园面积的最大值是255平方米．
科目：初中数学 来源： 题型：
【题目】如图，抛物线y=ax2+bx+c经过A（﹣1，0），B（4，0），C（0，3）三点，D为直线BC上方抛物线上一动点，DE⊥BC于E．
（1）求抛物线的函数表达式；
（2）如图1，求线段DE长度的最大值；
（3）如图2，设AB的中点为F，连接CD，CF，是否存在点D，使得△CDE中有一个角与∠CFO相等？若存在，求点D的横坐标；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
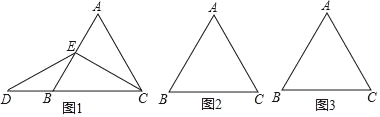
【题目】在等边三角形ABC中，E为直线AB上一点，连接EC．ED与直线BC交于点D，ED＝EC．
（1）如图1，AB＝1，点E是AB的中点，求BD的长；
（2）点E是AB边上任意一点（不与AB边的中点和端点重合），依题意，将图2补全，判断AE与BD间的数量关系并证明；
（3）点E不在线段AB上，请在图3中画出符合条件的一个图形．
查看答案和解析>>
科目：初中数学 来源： 题型：
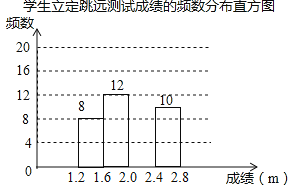
【题目】为了解某校九年级学生立定跳远水平，随机抽取该年级50名学生进行测试，并把测试成绩（单位：m）绘制成不完整的频数分布表和频数分布直方图．
学生立定跳远测试成绩的频数分布表
分组 | 频数 |
1.2≤x＜1.6 | a |
1.6≤x＜2.0 | 12 |
2.0≤x＜2.4 | b |
2.4≤x＜2.8 | 10 |
请根据图表中所提供的信息，完成下列问题：
（1）表中a= ，b= ，样本成绩的中位数落在 范围内；
（2）请把频数分布直方图补充完整；
（3）该校九年级共有1000名学生，估计该年级学生立定跳远成绩在2.4≤x＜2.8范围内的学生有多少人？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，OA，OD是⊙O半径．过A作⊙O的切线，交∠AOD的平分线于点C，连接CD，延长AO交⊙O于点E，交CD的延长线于点B．
(1)求证：直线CD是⊙O的切线；
(2)如果D点是BC的中点，⊙O的半径为 3cm，求
的长度．(结果保留π)
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】对任意一个正整数m，如果
，其中n是正整数，则称m为“优数”，n为m的最优拆分点，例如：
，则72是一个“优数”，8为72的最优拆分点．
请写出一个大于40小于50的“优数”______，它的最优拆分点是______．
把“优数”p的2倍与“优数”q的3倍的差记为
，例如：
，
，则
若“优数”p的最优拆分点为
，“优数”q的最优拆分点为t，当
时，求t的值并判断它是否为“优数”．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（12分）阅读理解：
如图①，如果四边形ABCD满足AB=AD，CB=CD，∠B=∠D=90°，那么我们把这样的四边形叫做“完美筝形”．
将一张如图①所示的“完美筝形”纸片ABCD先折叠成如图②所示形状，再展开得到图③，其中CE，CF为折痕，∠BCE=∠ECF=∠FCD，点B′为点B的对应点，点D′为点D的对应点，连接EB′，FD′相交于点O．
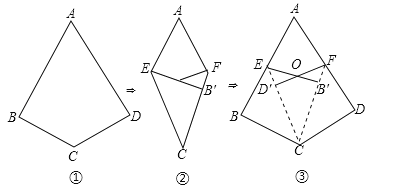
简单应用：
（1）在平行四边形、矩形、菱形、正方形四种图形中，一定为“完美筝形”的是 ；
（2）当图③中的∠BCD=120°时，∠AEB′= °；
（3）当图②中的四边形AECF为菱形时，对应图③中的“完美筝形”有 个（包含四边形ABCD）．
拓展提升：
（4）当图③中的∠BCD=90°时，连接AB′，请探求∠AB′E的度数，并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在一个不透明的袋子中，装有除颜色外都完全相同的4个红球和若干个黄球．
如果从袋中任意摸出一个球是红球的概率为
，那么袋中有黄球多少个？
在的条件下如果从袋中摸出一个球记下颜色后放回，再摸出一个球，用列表或画树状图的方法求出两次摸出不同颜色球的概率．
查看答案和解析>>
科目：初中数学 来源： 题型：
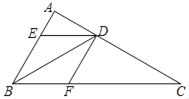
【题目】如图，BD是△ABC的角平分线，过点D作DE∥BC交AB于点E，DF∥AB交BC于点F．
（1）求证：四边形BEDF为菱形；
（2）如果∠A＝90°，∠C＝30°，BD＝6，求菱形BEDF的面积．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com