
ЁОЬтФПЁПНЋСНПщаББпГЄЯрЕШЕФЕШбќжБНЧШ§НЧАхАДШчЭМЂйАкЗХЃЌаББпABЗжБ№НЛCDЃЌCEгкMЃЌNЕуЃЎ
(1)ШчЙћАбЭМЂйжаЕФЁїBCNШЦЕуCФцЪБеыа§зЊ90ЁуЕУЕНЁїACFЃЌСЌНгFMЃЌШчЭМЂкЃЌЧѓжЄЃКЁїCMFЁеЁїCMNЃЛ
(2)НЋЁїCEDШЦЕуCа§зЊЃЌдђЃК
ЂйЕБЕуMЃЌNдкABЩЯ(ВЛгыЕуAЃЌBжиКЯ)ЪБЃЌЯпЖЮAMЃЌMNЃЌNBжЎМфгавЛИіВЛБфЕФЙиЯЕЪНЃЌЧыФуаДГіетИіЙиЯЕЪНЃЌВЂЫЕУїРэгЩЃЛ
ЂкЕБЕуMдкABЩЯЃЌЕуNдкABЕФбгГЄЯпЩЯ(ШчЭМЂл)ЪБЃЌЂйжаЕФЙиЯЕЪНЪЧЗёШдШЛГЩСЂЃП

ЁОД№АИЁП(1)МћНтЮіЃЛ(2)ЂйМћНтЮіЃЛЂкШдШЛГЩСЂЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОна§зЊЕФаджЪПЩЕУCF=CNЃЌЁЯACF=ЁЯBCNЃЌдйЧѓГіЁЯACM+ЁЯBCN=45ЁуЃЌДгЖјЧѓГіЁЯMCF=45ЁуЃЌШЛКѓРћгУЁАБпНЧБпЁБжЄУїЁїCMFКЭЁїCMNШЋЕШМДПЩЃЛ
ЃЈ2ЃЉЂйИљОнШЋЕШШ§НЧаЮЖдгІБпЯрЕШПЩЕУFM=MNЃЌдйИљОна§зЊЕФаджЪПЩЕУAF=BNЃЌЁЯCAF=ЁЯB=45ЁуЃЌДгЖјЧѓГіЁЯBAF=90ЁуЃЌдйРћгУЙДЙЩЖЈРэСаЪНМДПЩЕУНтЃЛ
ЂкАбЁїBCNШЦЕуCФцЪБеыа§зЊ90ЁуЕУЕНЁїACFЃЌИљОна§зЊЕФаджЪПЩЕУAF=BNCF=CNЃЌЁЯBCN=ЁЯACFЃЌдйЧѓГіЁЯMCF=ЁЯMCNЃЌШЛКѓРћгУЁАБпНЧБпЁБжЄУїЁїCMFКЭЁїCMNШЋЕШЃЌИљОнШЋЕШШ§НЧаЮЖдгІБпЯрЕШПЩЕУMF=MNЃЌШЛКѓРћгУЙДЙЩЖЈРэСаЪНМДПЩЕУНтЃЎ
ЃЈ1ЃЉЁпЁїBCNШЦЕуCФцЪБеыа§зЊ90ЁуЕУЕНЁїACFЃЌ
ЁрCF=CNЃЌЁЯACF=ЁЯBCNЃЌ
ЁпЁЯDCE=45ЁуЃЌ
ЁрЁЯACM+ЁЯBCN=45ЁуЃЌ
ЁрЁЯACM+ЁЯACF=45ЁуЃЌ
МДЁЯMCF=45ЁуЃЌ
ЁрЁЯMCF=ЁЯMCNЃЌ
дкЁїCMFКЭЁїCMNжаЃЌ
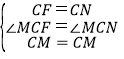 ЃЌ
ЃЌ
ЁрЁїCMFЁеЁїCMNЃЈSASЃЉЃЛ
ЃЈ2ЃЉЂйЁпЁїCMFЁеЁїCMNЃЌ
ЁрFM=MNЃЌ
гжЁпЁЯCAF=ЁЯB=45ЁуЃЌ
ЁрЁЯFAM=ЁЯCAF+ЁЯBAC=45Ёу+45Ёу=90ЁуЃЌ
ЁрAM2+AF2=FM2ЃЌ
ЁрAM2+BN2=MN2ЃЛ
ЂкШчЭМЃЌАбЁїBCNШЦЕуCФцЪБеыа§зЊ90ЁуЕУЕНЁїACFЃЌ
дђAF=BNЃЌCF=CNЃЌЁЯBCN=ЁЯACFЃЌ
ЁпЁЯMCF=ЁЯACB-ЁЯMCB-ЁЯACF=90Ёу-ЃЈ45Ёу-ЁЯBCNЃЉ-ЁЯACF=45Ёу+ЁЯBCN-ЁЯACF=45ЁуЃЌ
ЁрЁЯMCF=ЁЯMCNЃЌ
дкЁїCMFКЭЁїCMNжаЃЌ
 ЃЌ
ЃЌ
ЁрЁїCMFЁеЁїCMNЃЈSASЃЉЃЌ
ЁрFM=MNЃЌ
ЁпЁЯABC=45ЁуЃЌ
ЁрЁЯCAF=ЁЯCBN=135ЁуЃЌ
гжЁпЁЯBAC=45ЁуЃЌ
ЁрЁЯFAM=ЁЯCAF-ЁЯBAC=135Ёу-45Ёу=90ЁуЃЌ
ЁрAM2+AF2=FM2ЃЌ
ЁрAM2+BN2=MN2ЃЎ


 УћаЃПЮЬУЯЕСаД№АИ
УћаЃПЮЬУЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮвЙњЫЮГЏЪ§бЇМвбюЛддкЫћЕФжјзїЁЖЯъНтОХеТЫуЗЈЁЗжаЬсГіЁАбюЛдШ§НЧЁБЃЈШчЭМЃЉЃЌДЫЭМНвЪОСЫЃЈa+bЃЉnЃЈnЮЊЗЧИКећЪ§ЃЉеЙПЊЪНЕФЯюЪ§МАИїЯюЯЕЪ§ЕФгаЙиЙцТЩЃЎ
Р§ШчЃК
ЃЈa+bЃЉ0ЃН1
ЃЈa+bЃЉ1ЃНa+b
ЃЈa+bЃЉ2ЃНa2+2ab+b2
ЃЈa+bЃЉ3ЃНa3+3a2b+3ab2+b3
ЃЈa+bЃЉ4ЃНa4+4a3b+6a2b2+4ab3+b4
Ё
ЧыФуВТЯыЃЈa+bЃЉ9ЕФеЙПЊЪНжаЫљгаЯЕЪ§ЕФКЭЪЧЃЈЁЁЁЁЃЉ

A.2018B.512C.128D.64
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈ1ЃЉВйзїЃКШчЭМЃЌдквбжЊФкНЧЖШЪ§ЕФШ§ИіШ§НЧаЮжаЃЌЧыгУжБГпДгФГвЛЖЅЕуЛвЛЬѕЯпЖЮЃЌАбдШ§НЧаЮЗжИюГЩСНИіЕШбќШ§НЧаЮЃЌВЂдкЭМжаБъзЂЯргІЕФНЧЕФЖШЪ§

ЃЈ2ЃЉЭиеЙЃЌЁїABCжаЃЌAB=ACЃЌЁЯA=45ЁуЃЌЧыАбЁїABCЗжИюГЩШ§ИіЕШбќШ§НЧаЮЃЌВЂдкЭМжаБъзЂЯргІЕФНЧЕФЖШЪ§.

ЃЈ3ЃЉЫМПМдкШчЭМЫљЪОЕФШ§НЧаЮжаЁЯA=30Ёу.ЕуPКЭЕуQЗжБ№ЪЧБпACКЭBCЩЯЕФСНИіЖЏЕу.ЗжБ№СЌНгBPКЭPQАбЁїABCЗжИюГЩШ§ИіШ§НЧаЮ.ЁїABPЃЌЁїBPQЃЌЁїPQCШєЗжИюГЩЕФетШ§ИіШ§НЧаЮЖМЪЧЕШбќШ§НЧаЮЃЌЧѓЁЯCЕФЖШЪ§ЫљгаПЩФмжЕжБНгаДГіД№АИМДПЩ.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈ1ЃЉШчЭМ1ЃЌЫФБпаЮ![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЕу
ЃЌЕу![]() ЗжБ№дкБп
ЗжБ№дкБп![]() ЩЯЃЌЧв
ЩЯЃЌЧв![]() ЃЌЧѓжЄЃК
ЃЌЧѓжЄЃК![]() .
.

ЃЈ2ЃЉШчЭМ2ЃЌЫФБпаЮ![]() жаЃЌ
жаЃЌ![]() ЃЌЕу
ЃЌЕу![]() дкБп
дкБп![]() ЩЯЃЌСЌНг
ЩЯЃЌСЌНг![]() ЃЌ
ЃЌ![]() ЦНЗж
ЦНЗж![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌСЌНг
ЃЌСЌНг![]() .
.
ЂйевГіЭМжагы![]() ЯрЕШЕФЯпЖЮЃЌВЂМгвджЄУїЃЛ
ЯрЕШЕФЯпЖЮЃЌВЂМгвджЄУїЃЛ
ЂкЧѓ![]() ЕФЖШЪ§ЃЈгУКЌ
ЕФЖШЪ§ЃЈгУКЌ![]() ЕФЪНзгБэЪОЃЉ.
ЕФЪНзгБэЪОЃЉ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌAЃЈЉ3ЃЌ4ЃЉЃЌBЃЈЉ4ЃЌ1ЃЉЃЌCЃЈЉ1ЃЌ1ЃЉ

ЃЈ1ЃЉдкЭМжазїГіЁїABCЙигкxжсЕФжсЖдГЦЭМаЮЁїAЁфBЁфCЁфЃЛ
ЃЈ2ЃЉжБНгаДГіAЃЌBЙигкyжсЕФЖдГЦЕуAЁхЃЌBЁхЕФзјБъЃЛ
ЃЈ3ЃЉЧѓЁїABCЙигкyжсЕФжсЖдГЦЭМаЮЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌНЋОиаЮЃЈГЄЗНаЮЃЉ![]() би
би![]() елЕўЃЌЪЙЕу
елЕўЃЌЪЙЕу![]() гыЕу
гыЕу![]() жиКЯЃЌЕу
жиКЯЃЌЕу![]() Тфдк
Тфдк![]() ДІЃЌСЌНг
ДІЃЌСЌНг![]() ЃЌ
ЃЌ![]() ЃЌдђЯТСаНсТлЃКЂй
ЃЌдђЯТСаНсТлЃКЂй![]() ЃЌЂк
ЃЌЂк![]() ЃЌЂл
ЃЌЂл![]() ЃЌЂм
ЃЌЂм![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() Ш§ЕудкЭЌвЛжБЯпЩЯЃЌЦфжае§ШЗЕФЪЧЃЈ ЃЉ
Ш§ЕудкЭЌвЛжБЯпЩЯЃЌЦфжае§ШЗЕФЪЧЃЈ ЃЉ

A.ЂйЂкЂлB.ЂйЂлЂмC.ЂкЂлЂмD.ЂйЂкЂм
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌжБЯп![]() ЗжБ№НЛ
ЗжБ№НЛ![]() жсЁЂ
жсЁЂ![]() жсгкЕу
жсгкЕу![]() ЃЌЕу
ЃЌЕу![]() ЃЌЧв
ЃЌЧв![]() ЁЂ
ЁЂ![]() Тњзу
Тњзу![]() .
.
ЃЈ1ЃЉЧѓ![]() ЃЌ
ЃЌ![]() ЕФжЕ;
ЕФжЕ;
ЃЈ2ЃЉвд![]() ЮЊБпзї
ЮЊБпзї![]() ЃЌЕу
ЃЌЕу![]() дкжБЯп
дкжБЯп![]() ЕФгвВрЧв
ЕФгвВрЧв![]() ЃЌЧѓЕу
ЃЌЧѓЕу![]() ЕФзјБъЃЛ
ЕФзјБъЃЛ
ЃЈ3ЃЉШєЃЈ2ЃЉЕФЕу![]() дкЕкЫФЯѓЯоЃЈШчЭМ2ЃЉЃЌ
дкЕкЫФЯѓЯоЃЈШчЭМ2ЃЉЃЌ![]() гы
гы![]() НЛгкЕу
НЛгкЕу![]() ЃЌ
ЃЌ![]() гы
гы![]() жсНЛгкЕу
жсНЛгкЕу![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() НЛ
НЛ![]() жсгкЕу
жсгкЕу![]() .
.
ЂйЧѓжЄ![]() ;
;
ЂкжБНгаДГіЕу![]() ЕН
ЕН![]() ЕФОрРы.
ЕФОрРы.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌ![]() ЪЧБпГЄЮЊ6ЕФЕШБпШ§НЧаЮЃЌ
ЪЧБпГЄЮЊ6ЕФЕШБпШ§НЧаЮЃЌ![]() ЪЧ
ЪЧ![]() БпЩЯвЛЖЏЕуЃЌгЩ
БпЩЯвЛЖЏЕуЃЌгЩ![]() Яђ
Яђ![]() дЫЖЏЃЈгы
дЫЖЏЃЈгы![]() ЁЂ
ЁЂ![]() ВЛжиКЯЃЉЃЌ
ВЛжиКЯЃЉЃЌ![]() ЪЧ
ЪЧ![]() бгГЄЯпЩЯвЛЖЏЕуЃЌгыЕу
бгГЄЯпЩЯвЛЖЏЕуЃЌгыЕу![]() ЭЌЪБвдЯрЭЌЕФЫйЖШгЩ
ЭЌЪБвдЯрЭЌЕФЫйЖШгЩ![]() Яђ
Яђ![]() бгГЄЯпЗНЯђдЫЖЏЃЈ
бгГЄЯпЗНЯђдЫЖЏЃЈ![]() ВЛгы
ВЛгы![]() жиКЯЃЉЃЌЙ§
жиКЯЃЉЃЌЙ§![]() зї
зї![]() гк
гк![]() ЃЌСЌНг
ЃЌСЌНг![]() НЛ
НЛ![]() гк
гк![]() .
.

ЃЈ1ЃЉЕБ![]() ЪБЃЌЧѓ
ЪБЃЌЧѓ![]() ЕФГЄЃЛ
ЕФГЄЃЛ
ЃЈ2ЃЉдкдЫЖЏЙ§ГЬжаЯпЖЮ![]() ЕФГЄЪЧЗёЗЂЩњБфЛЏЃПШчЙћВЛБфЃЌЧѓГіЯпЖЮ
ЕФГЄЪЧЗёЗЂЩњБфЛЏЃПШчЙћВЛБфЃЌЧѓГіЯпЖЮ![]() ЕФГЄЃЛШчЙћЗЂЩњИФБфЃЌЧыЫЕУїРэгЩ.
ЕФГЄЃЛШчЙћЗЂЩњИФБфЃЌЧыЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдке§ЗНаЮABCDжаЃЌЕуEЁЂFЗжБ№дкBCЁЂCDЩЯЃЌЁїAEFЪЧЕШБпШ§НЧаЮЃЌСЌНгACНЛEFгкЕуGЃЌЯТСаНсТлЃКЂй![]() ЃЛЂкAG=
ЃЛЂкAG=![]() GCЃЛЂлBE+DF=EFЃЛЂм
GCЃЛЂлBE+DF=EFЃЛЂм![]() .Цфжае§ШЗЕФЪЧЃЈ ЃЉ
.Цфжае§ШЗЕФЪЧЃЈ ЃЉ

A.ЂйЂкЂлB.ЂйЂлЂмC.ЂйЂкЂмD.ЂйЂкЂлЂм
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com