
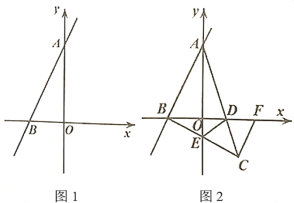
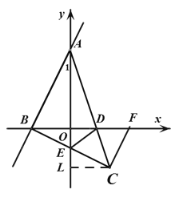
【题目】如图1,在平面直角坐标系中,直线![]() 分别交
分别交![]() 轴、
轴、![]() 轴于点
轴于点![]() ,点
,点![]() ,且
,且![]() 、
、![]() 满足
满足![]() .
.
(1)求![]() ,
,![]() 的值;
的值;
(2)以![]() 为边作
为边作![]() ,点
,点![]() 在直线
在直线![]() 的右侧且
的右侧且![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)若(2)的点![]() 在第四象限(如图2),
在第四象限(如图2),![]() 与
与![]() 交于点
交于点![]() ,
,![]() 与
与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() 交
交![]() 轴于点
轴于点![]() .
.
①求证![]() ;
;
②直接写出点![]() 到
到![]() 的距离.
的距离.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() 或
或![]() ;(3)①见解析,②
;(3)①见解析,②![]()
【解析】
(1)将等式![]() 变形后,利用非负数的性质即可得到a,b的值;
变形后,利用非负数的性质即可得到a,b的值;
(2)由题意分![]() 和
和![]() 两种情况讨论,当
两种情况讨论,当![]() 时,过点
时,过点![]() 作
作![]() 于
于![]() ,利用AAS证
,利用AAS证![]() ,从而求得点C的坐标;当
,从而求得点C的坐标;当![]() 时,同理可得解;
时,同理可得解;
(3)①过点![]() 作
作![]() 轴于点
轴于点![]() ,依次证得
,依次证得![]()
![]() ,
,![]()
![]() ,即可得证
,即可得证![]() ;
;
②过点C分别作x轴、DL的垂线,交于点K、H,通过证明△EDC≌△FDC得到∠DEC =∠LEC,再利用角平分线的性质定理得到CH=CL=1.
.解:(1)![]()
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ;
;
(2)由(1)知![]() ,
,![]() ,
,
![]() ,
,![]()
![]() ,
,![]() ,
,
![]() 是直角三角形,且
是直角三角形,且![]() ,
,
![]() 只有
只有![]() 或
或![]() ,
,
Ⅰ、当![]() 时,如图,
时,如图,
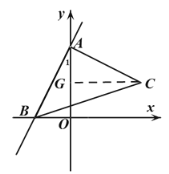
![]() ,
,
![]() ,
,
过点![]() 作
作![]() 于
于![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,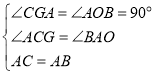
![]()
![]() ,
,
![]() ,
,![]()
![]() ,
,
![]() ,
,
Ⅱ、当![]() 时,如图
时,如图
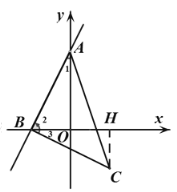
同Ⅰ的方法得,![]() ;
;
即:满足条件的点![]() 或
或![]()
(3)①如图,由(2)知点![]() ,
,
过点![]() 作
作![]() 轴于点
轴于点![]() ,则
,则![]()
在![]() 和
和![]() 中,
中,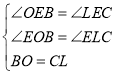
![]()
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,
![]()
![]() ,
,
![]() ,
,
![]() ;
;
②CH=![]() ,
,
如图,过点C分别作x轴、y轴、DE的垂线,交于点K、L、H,
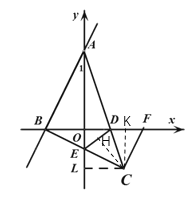
由①可知,CL=CK=1,
∠ECL+∠DCK=∠LCK-∠ECD=90°-45°=45°,
∠FCK+∠KCD=∠ECF-∠ECD=90°-45°=45°,
∴∠ECL=∠FCK,又∠FKC=∠ELC=90°,
∴△ELC≌△FKC(AAS),
∴∠LEC=∠KFC,EC=FC,
∠FCD=∠FCK+∠KCD=∠ECL+∠KCD=45°=∠ECD,
又CD=CD,
∴△EDC≌△FDC(SAS),
∴∠DEC=∠DFC,
∴∠DEC =∠LEC.
又![]()
∴CH=CL=1


科目:初中数学 来源: 题型:
【题目】如图,一电线杆AB的影子分别落在了地上和墙上.同一时刻,小明竖起1米高的直杆MN,量得其影长MF为0.5米,量得电线杆AB落在地上的影子BD长3米,落在墙上的影子CD的高为2米.你能利用小明测量的数据算出电线杆AB的高吗?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等边三角形ABC中,D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转60°,得到△BAE,连接ED,若BC=5,BD=4,有下列结论:①AE∥BC;②∠ADE=∠BDC;③△BDE是等边三角形;④△ADE的周长是9.其中,正确结论的个数是( )

A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将两块斜边长相等的等腰直角三角板按如图①摆放,斜边AB分别交CD,CE于M,N点.
(1)如果把图①中的△BCN绕点C逆时针旋转90°得到△ACF,连接FM,如图②,求证:△CMF≌△CMN;
(2)将△CED绕点C旋转,则:
①当点M,N在AB上(不与点A,B重合)时,线段AM,MN,NB之间有一个不变的关系式,请你写出这个关系式,并说明理由;
②当点M在AB上,点N在AB的延长线上(如图③)时,①中的关系式是否仍然成立?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张康和李健两名运动爱好者周末相约到丹江环库绿道进行跑步锻炼.
(1)周日早上![]() 点,张康和李健同时从家出发,分别骑自行车和步行到离家距离分别为
点,张康和李健同时从家出发,分别骑自行车和步行到离家距离分别为![]() 千米和
千米和![]() 千米的绿道环库路入口汇合,结果同时到达,且张康每分钟比李健每分钟多行
千米的绿道环库路入口汇合,结果同时到达,且张康每分钟比李健每分钟多行![]() 米,求张康和李健的速度分别是多少米
米,求张康和李健的速度分别是多少米![]() 分?
分?
(2)两人到达绿道后约定先跑![]() 千米再休息,李健的跑步速度是张康跑步速度的
千米再休息,李健的跑步速度是张康跑步速度的![]() 倍,两人在同起点,同时出发,结果李健先到目的地
倍,两人在同起点,同时出发,结果李健先到目的地![]() 分钟.
分钟.
①当![]() ,
,![]() 时,求李健跑了多少分钟?
时,求李健跑了多少分钟?
②求张康的跑步速度多少米![]() 分?(直接用含
分?(直接用含![]() ,
,![]() 的式子表示)
的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个安装有进出水管的30升容器,水管单位时间内进出的水量是一定的,设从
某时刻开始的4分钟内只进水不出水,在随后的8分钟内既进水又出水,得到水量y(升)
与时间x(分)之间的函数关系如图所示.根据图象信息给出下列说法:
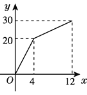
①每分钟进水5升;②当4≤x≤12时,容器中水量在减少;
③若12分钟后只放水,不进水,还要8分钟可以把水放完;
④若从一开始进出水管同时打开需要24分钟可以将容器灌满.
以上说法中正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
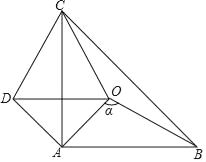
【题目】如图,△ABC和△AOD是等腰直角三角形,AB=AC,AO=AD,∠BAC=∠OAD=90°,点O是△ABC内的一点,∠BOC=130°.
(1)求证:OB=DC;
(2)求∠DCO的大小;
(3)设∠AOB=α,那么当α为多少度时,△COD是等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在![]() 和
和![]() 中,
中, ![]() ,
,![]() ,
,![]() .
.

(1)若![]() 三点在同一直线上,连接
三点在同一直线上,连接![]() 交
交![]() 于点
于点![]() ,求证:
,求证: ![]() .
.
(2)在第(1)问的条件下,求证: ![]() ;
;
(3)将![]() 绕点
绕点![]() 顺时针旋转得到图2,那么第(2)问中的结论是否依然成立?若成立,请证明你的结论:若不成立,请说明理由.
顺时针旋转得到图2,那么第(2)问中的结论是否依然成立?若成立,请证明你的结论:若不成立,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com