
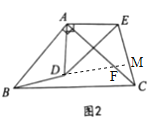
【题目】如图1,在![]() 和
和![]() 中,
中, ![]() ,
,![]() ,
,![]() .
.

(1)若![]() 三点在同一直线上,连接
三点在同一直线上,连接![]() 交
交![]() 于点
于点![]() ,求证:
,求证: ![]() .
.
(2)在第(1)问的条件下,求证: ![]() ;
;
(3)将![]() 绕点
绕点![]() 顺时针旋转得到图2,那么第(2)问中的结论是否依然成立?若成立,请证明你的结论:若不成立,请说明理由.
顺时针旋转得到图2,那么第(2)问中的结论是否依然成立?若成立,请证明你的结论:若不成立,请说明理由.
【答案】(1)见解析;(2)见解析;(3)成立,理由见解析
【解析】
(1)根据SAS得出△BAD≌△CAE;
(2)根据△BAD≌△CAE,得出∠ABD=∠ACE,根据直角三角形两锐角互余和对顶角相等即可得出答案;
(3)延长BD交CE于点M,交AC于点F.根据SAS证明ΔBAD≌ΔCAE,得出∠ABD=∠ACE,根据直角三角形两锐角互余和对顶角相等即可得出答案.
(1)∵∠BAC=∠DAE=90°,
∴∠BAC+∠CAD=∠DAE+∠CAD,
即∠BAD=∠CAE.
∵AB=AC,AD=AE,
∴ΔBAD≌ΔCAE.
(2)∵ΔBAD≌ΔCAE,
∴∠ABD=∠ACE.
∵∠BAC=90°,
∴∠ABD+∠AFB=90°.
∵∠AFB=∠CFD,
∴∠ACE+∠CFD=90°,
∴∠CDF=90°,
∴BD⊥CE.
(3)成立.理由如下:
延长BD交CE于点M,交AC于点F.
∵∠BAC=∠DAE=90°,
∴∠BAC-∠CAD=∠DAE-∠CAD,
即∠BAD=∠CAE.
∵AB=AC,AD=AE,
∴ΔBAD≌ΔCAE,
∴∠ABD=∠ACE.
∵∠BAC=90°,
∴∠ABD+∠AFB=90°.
∵∠AFB=∠CFM,
∴∠CMF=90°,
∴BD⊥CE.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,BD⊥AC于点D.
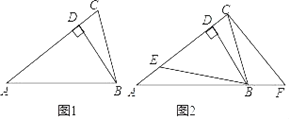
(1)若∠C=∠ABC=2∠A,则∠DBC= °;
(2)若∠A=2∠CBD,求证:∠ACB=∠ABC;
(3)如图2,在(2)的条件下,E是AD上一点,F是AB延长线上一点,连接BE、CF,使∠BEC=∠CFB,∠BCF=2∠ABE,求∠EBC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“友谊商场”某种商品平均每天可销售100件,每件盈利20元.“五一”期间,商场决定采取适当的降价措施.经调查发现,每件该商品每降价1元,商场平均每天可多售出10件.设每件商品降价x元,请回答:
(1)降价后每件商品盈利元,商场日销售量件(用含x的代数式表示);
(2)求每件商品降价多少元时,商场日盈利可达到最大?最大日盈利是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A(2,0),D(6,4),将线段AD平移得到BC,B(0,﹣6),延长BC交x轴于点E.
(1)则△ABC的面积是 ;
(2)Q为x轴上一动点,当△ABC与△ADQ的面积相等时,试求点Q的坐标.
(3)若存在一点M(m,6)且△ADM的面积不小于△ABC的面积,求m的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c的顶点为D(﹣1,2),与x轴的一个交点A在点(﹣3,0)和(﹣2,0)之间,其部分图象如图,则以下结论:①b2﹣4ac<0;②a+b+c<0;③c﹣a=2;④方程ax2+bx+c﹣2=0有两个相等的实数根.其中正确的结论有(填序号). 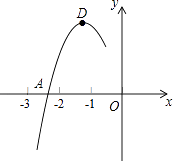
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD∥BC,FC⊥CD,∠1=∠2,∠B=60°.

(1)求∠BCF的度数;(2)如果DE是∠ADC的平分线,那么DE与AB平行吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,点M、N分别在AB,BC上,将△BMN沿MN翻折,得△FMN,若MF∥AD,FN∥DC,∠A=100°,∠C=70°,则∠B= . 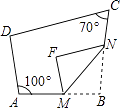
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com