
【题目】已知抛物线 ![]() 经过
经过 ![]() 两点.
两点.
(1)求抛物线的解析式和顶点坐标;
(2)设点 ![]() 为抛物线上一点,若
为抛物线上一点,若 ![]() ,求点
,求点 ![]() 的坐标.
的坐标.
【答案】
(1)解:把A(-1,0)、B(3,0)分别代入y=x2+bx+c中,
得: ![]() ,
,
解得: ![]() ,
,
∴抛物线的解析式为y=x2-2x-3.
∵y= x2-2x-3=(x-1)2-4,
∴顶点坐标为(1,-4)
(2)解:∵A(-1,0)、B(3,0),∴AB=4.
设P(x,y),则S△PAB= ![]() AB|y|=2|y|=6,
AB|y|=2|y|=6,
∴|y|=3,
∴y=±3.
①当y=3时,x2-2x-3=3,解得:x1=1+ ![]() ,x2=1-
,x2=1- ![]() ,
,
此时P点坐标为(1+ ![]() ,3)或(1-
,3)或(1- ![]() ,3);
,3);
②当y=-3时,x2-2x-3=-3,解得:x1=0,x2=2,
此时P点坐标为(0,-3)或(2,-3).
综上所述,P点坐标为(1+ ![]() ,3)或(1-
,3)或(1- ![]() ,3)或(0,-3)或(2,-3)
,3)或(0,-3)或(2,-3)
【解析】利用二次函数的知识进行求解,)将A与B的坐标代入抛物线的解析式即可求出b与c的值.设P(x,y),△PAB的高为|y|,AB=4,由S△PAB=6列出方程即可求出y的值,从而可求出P的坐标.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在等边△ABC中,点D在BC边上,点E在AC的延长线上,DE=DA(如图1).
(1)求证:∠BAD=∠EDC;
(2)若点E关于直线BC的对称点为M(如图2),连接DM,AM.求证:DA=AM.
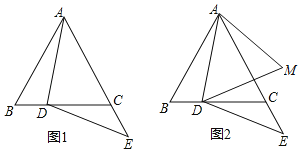
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】竖直上抛的小球离地高度是它运动时间的二次函数,小军相隔1秒依次竖直向上抛出两个小球,假设两个小球离手时离地高度相同,在各自抛出后1.1秒时到达相同的最大离地高度,第一个小球抛出后t秒时在空中与第二个小球的离地高度相同,则t= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△DBC中,∠A=40°,AB=AC=2,∠BDC=140°,BD=CD,以点D为顶点作∠MDN=70°,两边分别交AB,AC于点M,N,连接MN,则△AMN的周长为___________.
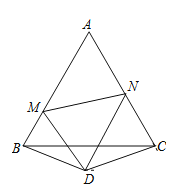
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某小区要用篱笆围成一矩形花坛,花坛的一边用足够长的墙,另外三边所用的篱笆之和恰好为 ![]() 米.
米.
(1)求矩形 ![]() 的面积(用
的面积(用 ![]() 表示,单位:平方米)与边
表示,单位:平方米)与边 ![]() (用
(用 ![]() 表示,单位:米)之间的函数关系式(不要求写出自变量
表示,单位:米)之间的函数关系式(不要求写出自变量 ![]() 的取值范围);怎样围,可使花坛面积最大?
的取值范围);怎样围,可使花坛面积最大?
(2)如何围,可使此矩形花坛面积是 ![]() 平方米?
平方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在![]() 和
和![]() 中,
中, ![]() ,
,![]() ,
,![]() .
.

(1)若![]() 三点在同一直线上,连接
三点在同一直线上,连接![]() 交
交![]() 于点
于点![]() ,求证:
,求证: ![]() .
.
(2)在第(1)问的条件下,求证: ![]() ;
;
(3)将![]() 绕点
绕点![]() 顺时针旋转得到图2,那么第(2)问中的结论是否依然成立?若成立,请证明你的结论:若不成立,请说明理由.
顺时针旋转得到图2,那么第(2)问中的结论是否依然成立?若成立,请证明你的结论:若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读并解答问题:
明朝数学家程大位在其数学著作《直指算法统宗》中以《西江月》词牌叙述了一道“荡秋千”问题:原文:平地秋千未起,踏板一尺离地.送行二步与人齐,五尺人高曾记.仕女佳人争蹴,终朝笑语欢嬉.良工高士素好奇,算出索长有几?译文:如图,有一架秋千,当它静止时,踏板离地![]() 尺,将它往前推送
尺,将它往前推送![]() 尺(水平距离)时,秋千的踏板就和人一样高,这个人的身高为
尺(水平距离)时,秋千的踏板就和人一样高,这个人的身高为![]() 尺,秋千的绳索始终拉得很直,试问绳索有多长?(注:古代
尺,秋千的绳索始终拉得很直,试问绳索有多长?(注:古代![]() 尺为
尺为![]() 步)
步)

建立数学模型:如图,秋千绳索![]() 静止的时候,踏板离地高
静止的时候,踏板离地高![]() 尺(
尺(![]() 尺),将它往前推进两步(
尺),将它往前推进两步(![]() 尺),此时踏板升高离地
尺),此时踏板升高离地![]() 尺(
尺(![]() 尺).已知
尺).已知![]() 于点
于点![]() 于点
于点![]() 于点
于点![]() ,点
,点![]() 在
在![]() 上,
上,![]() ,求秋千绳索(
,求秋千绳索(![]() 或
或![]() )的长度.请解答下列问题:
)的长度.请解答下列问题:
(1)直接写出四边形![]() 是哪种特殊的四边形;
是哪种特殊的四边形;
(2)求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数 ![]() 的图象与一次函数
的图象与一次函数 ![]() 的图象交于点A(1,4)、点B(-4,n).
的图象交于点A(1,4)、点B(-4,n).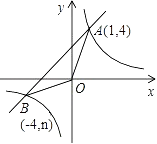
(1)求 ![]() 和
和 ![]() 的值;
的值;
(2)求△OAB的面积;
(3)直接写出一次函数值大于反比例函数值的自变量 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知D、E在△ABC的边上,DE∥BC,∠B=60°,∠AED=40°,则∠A的度数为( )
A.100°
B.90°
C.80°
D.70°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com