
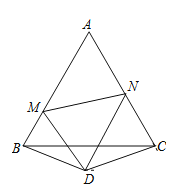
【题目】如图,在△ABC和△DBC中,∠A=40°,AB=AC=2,∠BDC=140°,BD=CD,以点D为顶点作∠MDN=70°,两边分别交AB,AC于点M,N,连接MN,则△AMN的周长为___________.
【答案】4
【解析】
延长AC至E,使CE=BM,连接DE.证明△BDM≌△CDE(SAS),得出MD=ED,∠MDB=∠EDC,证明△MDN≌△EDN(SAS),得出MN=EN=CN+CE,进而得出答案.
延长AC至E,使CE=BM,连接DE.
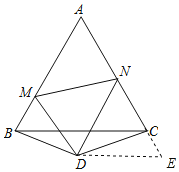
∵BD=CD,且∠BDC=140°,
∴∠DBC=∠DCB=20°,
∵∠A=40°,AB=AC=2,
∴∠ABC=∠ACB=70°,
∴∠MBD=∠ABC+∠DBC=90°,
同理可得∠NCD=90°,
∴∠ECD=∠NCD=∠MBD=90°,
在△BDM和△CDE中,
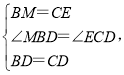
∴△BDM≌△CDE(SAS),
∴MD=ED,∠MDB=∠EDC,
∴∠MDE=∠BDC=140°,
∵∠MDN=70°,
∴∠EDN=70°=∠MDN,
在△MDN和△EDN中,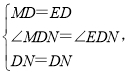
∴△MDN≌△EDN(SAS),
∴MN=EN=CN+CE,
∴△AMN的周长=AM+MN+AN=AM+CN+CE+AN=AM+AN+CN+BM=AB+AC=4;
故答案为:4.


科目:初中数学 来源: 题型:
【题目】为适应日益激烈的市场竞争要求,某工厂从2016年1月且开始限产,并对生产线进行为期5个月的升降改造,改造期间的月利润与时间成反比例;到5月底开始恢复全面生产后,工厂每月的利润都比前一个月增加10万元.设2016年1月为第1个月,第x个月的利润为y万元,其图象如图所示,试解决下列问题: 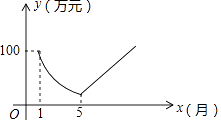
(1)分别求该工厂对生产线进行升级改造前后,y与x之间的函数关系式;
(2)到第几个月时,该工厂月利润才能再次达到100万元?
(3)当月利润少于50万元时,为该工厂的资金紧张期,问该工厂资金紧张期共有几个月?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是高,AE是角平分线.
(1)若∠B=30°,∠C=70°,则∠CAE=______°,∠DAE=______°.
(2>若∠B=40°,∠C=80°.则∠DAE=______°.
(3)通过探究,小明发现将(2)中的条件“∠B=40°,∠C=80°”改为“∠C-∠B=40°”,也求出了∠DAE的度数,请你写出小明的求解过程.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“友谊商场”某种商品平均每天可销售100件,每件盈利20元.“五一”期间,商场决定采取适当的降价措施.经调查发现,每件该商品每降价1元,商场平均每天可多售出10件.设每件商品降价x元,请回答:
(1)降价后每件商品盈利元,商场日销售量件(用含x的代数式表示);
(2)求每件商品降价多少元时,商场日盈利可达到最大?最大日盈利是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A(2,0),D(6,4),将线段AD平移得到BC,B(0,﹣6),延长BC交x轴于点E.
(1)则△ABC的面积是 ;
(2)Q为x轴上一动点,当△ABC与△ADQ的面积相等时,试求点Q的坐标.
(3)若存在一点M(m,6)且△ADM的面积不小于△ABC的面积,求m的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】古埃及人曾经用如图所示的方法画直角:把一根长绳打上等距离的13 个结,然后以3个结间距、4 个结间距、5 个结间距的长度为边长,用木桩钉成一个三角形,其中一角便是直角,这样做的道理是( )
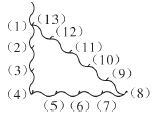
A.直角三角形两个锐角互补
B.三角形内角和等于180°
C.三角形两条短边的平方和等于长边的平方
D.如果三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com