
【题目】如图,已知反比例函数 ![]() 的图象与一次函数
的图象与一次函数 ![]() 的图象交于点A(1,4)、点B(-4,n).
的图象交于点A(1,4)、点B(-4,n).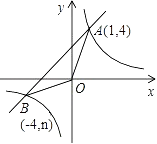
(1)求 ![]() 和
和 ![]() 的值;
的值;
(2)求△OAB的面积;
(3)直接写出一次函数值大于反比例函数值的自变量 ![]() 的取值范围.
的取值范围.
【答案】
(1)解:把A点(1,4)分别代入反比例函数y=![]() ,一次函数y=x+b,
,一次函数y=x+b,
得k=1×4,1+b=4,解得k=4,b=3,
∴反比例函数的解析式是y=![]() ,一次函数解析式是y=x+3;
,一次函数解析式是y=x+3;
(2)解:如图,设直线y=x+3与y轴的交点为C,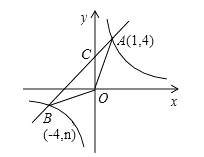
当x=-4时,y=-1,∴B(-4,-1),当x=0时,y=+3,∴C(0,3),
∴S△AOB=S△AOC+S△BOC=×3×4+×3×1=15/2
(3)解:∵B(-4,-1),A(1,4),
∴根据图象可知:当x>1或-4<x<0时,一次函数值大于反比例函数值.
【解析】(1)将点A的坐标分别代入两函数解析式,求出k、b的值,即可求出函数解析式。
(2)先求出点B的坐标,再求出直线AB与y轴的交点C的坐标,再根据S△AOB=S△AOC+S△BOC计算即可得出结果。
(3)观察直线x=-4、y轴、直线x=1这三条直线将两图像分成四部分,由图像观察一次函数的图像高于反比例函数的图像,写出取值范围即可。


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是高,AE是角平分线.
(1)若∠B=30°,∠C=70°,则∠CAE=______°,∠DAE=______°.
(2>若∠B=40°,∠C=80°.则∠DAE=______°.
(3)通过探究,小明发现将(2)中的条件“∠B=40°,∠C=80°”改为“∠C-∠B=40°”,也求出了∠DAE的度数,请你写出小明的求解过程.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某篮球队在一次联赛中共进行了10场比赛,已知这10场比赛的平均得分为48分,且前9场比赛的得分依次为:57,51,45,51,44,46,45,42,48.
(1)求第10场比赛的得分;
(2)直接写出这10场比赛的中位数,众数和方差.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD∥BC,FC⊥CD,∠1=∠2,∠B=60°.

(1)求∠BCF的度数;(2)如果DE是∠ADC的平分线,那么DE与AB平行吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市的连锁超市总部为了解各超市的销售情况,统计了各超市在某月的销售额(单位:万元),并根据统计的这组销售额数据,绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:
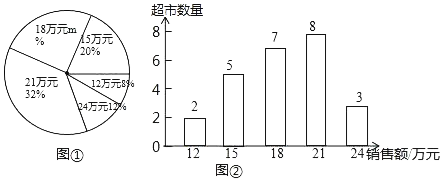
(I)该市的连锁超市总数为 ,图①中m的值为 ;
(II)求统计的这组销售额数据的平均数、众数和中位数.
查看答案和解析>>
科目:初中数学 来源: 题型:
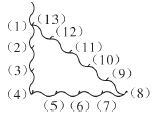
【题目】古埃及人曾经用如图所示的方法画直角:把一根长绳打上等距离的13 个结,然后以3个结间距、4 个结间距、5 个结间距的长度为边长,用木桩钉成一个三角形,其中一角便是直角,这样做的道理是( )
A.直角三角形两个锐角互补
B.三角形内角和等于180°
C.三角形两条短边的平方和等于长边的平方
D.如果三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,∠1=∠2,则不一定能使△ABD≌△ACD的条件是 ( )

A. AB=AC B. BD=CD C. ∠B=∠C D. ∠BDA=∠CDA
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com