
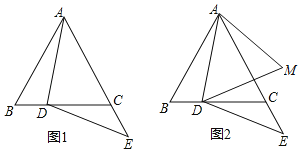
【题目】在等边△ABC中,点D在BC边上,点E在AC的延长线上,DE=DA(如图1).
(1)求证:∠BAD=∠EDC;
(2)若点E关于直线BC的对称点为M(如图2),连接DM,AM.求证:DA=AM.
【答案】(1)见解析;(2)见解析
【解析】
(1)根据等边三角形的性质,得出∠BAC=∠ACB=60°,然后根据三角形的内角和和外角性质,进行计算即可.
(2)根据轴对称的性质,可得DM=DA,然后结合(1)可得∠MDC=∠BAD,然后根据三角形的内角和,求出∠ADM=60°即可.
解:(1)如图1,
∵△ABC是等边三角形,∴∠BAC=∠ACB=60°,
∴∠BAD=60°﹣∠DAE,∠EDC=60°﹣∠E,
又∵DE=DA,
∴∠E=∠DAE,
∴∠BAD=∠EDC.
(2)由轴对称可得,DM=DE,∠EDC=∠MDC,
∵DE=DA,
∴DM=DA,
由(1)可得,∠BAD=∠EDC,
∴∠MDC=∠BAD,
∵△ABD中,∠BAD+∠ADB=180°﹣∠B=120°,
∴∠MDC+∠ADB=120°,
∴∠ADM=60°,
∴△ADM是等边三角形,
∴AD=AM.


科目:初中数学 来源: 题型:
【题目】如图,在半径为6cm的⊙O中,点A是劣弧 ![]() 的中点,点D是优弧
的中点,点D是优弧 ![]() 上一点,且∠D=30下列四个结论:①OA⊥BC;②BC=
上一点,且∠D=30下列四个结论:①OA⊥BC;②BC= ![]() cm;③cos∠AOB=
cm;③cos∠AOB= ![]() ;④四边形ABOC是菱形.其中正确结论的序号是( )
;④四边形ABOC是菱形.其中正确结论的序号是( )
A.①③
B.①②③④
C.①②④
D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在横线上完成下面的证明,并在括号内注明理由.
已知:如图,∠ABC+∠BGD=180°,∠1=∠2.
求证:EF∥DB.
证明:∵∠ABC+∠BGD=180°,(已知)
∴ .( )
∴∠1=∠3.( )
又∵∠1=∠2,(已知)
∴ .( )
∴EF∥DB.( )

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为适应日益激烈的市场竞争要求,某工厂从2016年1月且开始限产,并对生产线进行为期5个月的升降改造,改造期间的月利润与时间成反比例;到5月底开始恢复全面生产后,工厂每月的利润都比前一个月增加10万元.设2016年1月为第1个月,第x个月的利润为y万元,其图象如图所示,试解决下列问题: 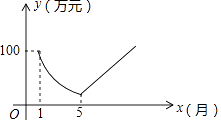
(1)分别求该工厂对生产线进行升级改造前后,y与x之间的函数关系式;
(2)到第几个月时,该工厂月利润才能再次达到100万元?
(3)当月利润少于50万元时,为该工厂的资金紧张期,问该工厂资金紧张期共有几个月?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】共有1500kg化工原料,由A,B两种机器人同时搬运,其中,A型机器人比B型机器每小时多搬运30kg,A型机器人搬运900kg所用时间与B型机器人搬运600kg所用时间相等,问需要多长时间才能运完?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,BD⊥AC于点D.
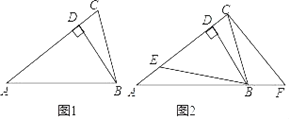
(1)若∠C=∠ABC=2∠A,则∠DBC= °;
(2)若∠A=2∠CBD,求证:∠ACB=∠ABC;
(3)如图2,在(2)的条件下,E是AD上一点,F是AB延长线上一点,连接BE、CF,使∠BEC=∠CFB,∠BCF=2∠ABE,求∠EBC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣x2+2x+k+2与x轴的公共点有两个.
(1)求k的取值范围;
(2)当k=1时,求抛物线与x轴的公共点A和B的坐标及顶点C的坐标;
(3)观察图象,当x取何值时y>0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是高,AE是角平分线.
(1)若∠B=30°,∠C=70°,则∠CAE=______°,∠DAE=______°.
(2>若∠B=40°,∠C=80°.则∠DAE=______°.
(3)通过探究,小明发现将(2)中的条件“∠B=40°,∠C=80°”改为“∠C-∠B=40°”,也求出了∠DAE的度数,请你写出小明的求解过程.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com