
【题目】已知二次函数y=﹣x2+2x+k+2与x轴的公共点有两个.
(1)求k的取值范围;
(2)当k=1时,求抛物线与x轴的公共点A和B的坐标及顶点C的坐标;
(3)观察图象,当x取何值时y>0.
【答案】
(1)解:∵二次函数y=﹣x2+2x+k+2与x轴有两个交点.
∴△=22﹣4×(﹣1)×(k+2)>0
解得:k>﹣3;
(2)解:当k=1时,二次函数是y=﹣x2+2x+3,
令y=0,得﹣x 2+2x+3=0,
解得:x 1=﹣1,x 2=3
∴抛物线与X轴的公共点A、B的坐标分别是(﹣1,0)、(3,0),
∵y=﹣x 2+2x+3=﹣(x﹣1)2+4
∴抛物线的顶点C的坐标是(1,4)
(3)解:由图象可知:当x=﹣1或x=3时,y=0;
当﹣1<x<3时,y>0.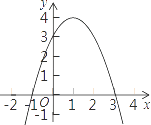
【解析】(1)抓住已知二次函数与x轴有两个交点得出b2-4ac>0,列不等式求出解集即可。
(2)将k=1代入函数解析式求出二次函数解析式,再根据y=0,解关于x的一元二次方程,求出x的值,就可得出抛物线与X轴的公共点A、B的坐标;然后将二次函数解析式配方成y=a(x-h)2+k的形式,就可求出其顶点坐标。
(3)先根据顶点坐标,抛物线与x轴的交点坐标、抛物线与y轴的交点坐标画出函数图像,再观察图像y>0,即是观察x轴上方的图像,就可写出自变量的取值范围。


 名师点拨卷系列答案
名师点拨卷系列答案科目:初中数学 来源: 题型:
【题目】如图,AC是⊙O的直径,BC是⊙O的弦,点P是⊙O外一点,连接PB、AB,∠PBA=∠C.
(1)求证:PB是⊙O的切线;
(2)连接OP,若OP∥BC,且OP=8,⊙O的半径为2 ![]() ,求BC的长.
,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解九年级学生的视力情况,随机抽样调查了部分九年级学生的视力,以下是根据调查结果绘制的统计图表的一部分.
分组 | 视力 | 人数 |
A | 3.95≤x≤4.25 | 3 |
B | 4.25<x≤4.55 |
|
C | 4.55<x≤4.85 | 18 |
D | 4.85<x≤5.15 | 8 |
E | 5.15<x≤5.45 |
|
根据以上信息,解谷下列问题:
(1)在被调查学生中,视力在3.95≤x≤4.25范围内的人数为 人;
(2)本次调查的样本容量是 ,视力在5.15<x≤5.45范围内学生数占被调查学生数的百分比是 %;
(3)在统计图中,C组对应扇形的圆心角度数为 °;
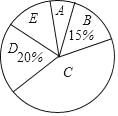
(4)若该校九年级有400名学生,估计视力超过4.85的学生数.
查看答案和解析>>
科目:初中数学 来源: 题型:
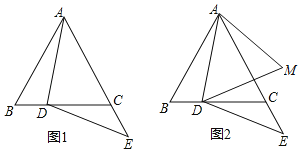
【题目】在等边△ABC中,点D在BC边上,点E在AC的延长线上,DE=DA(如图1).
(1)求证:∠BAD=∠EDC;
(2)若点E关于直线BC的对称点为M(如图2),连接DM,AM.求证:DA=AM.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校学生会向全校![]() 名学生发起了爱心捐款活动,为了解捐款情况,学生会随机调查了部分学生的捐款金额,并用得到的数据绘制了如下统计图1和图2,请根据相关信息,解答下列问题:
名学生发起了爱心捐款活动,为了解捐款情况,学生会随机调查了部分学生的捐款金额,并用得到的数据绘制了如下统计图1和图2,请根据相关信息,解答下列问题:
(1)本次接受随机抽样调查的学生人数为 人,图![]() 中
中![]() 的值是 .
的值是 .
(2)补全图2的统计图.
(3)求本次调查获取的样本数据的平均数、众数和中位数;
(4)根据样本数据,估计该校本次活动捐款金额为![]() 元的学生人数.
元的学生人数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+(k﹣5)x+1﹣k=0,其中k为常数.
(1)求证:无论k为何值,方程总有两个不相等实数根;
(2)已知函数y=x2+(k﹣5)x+1﹣k的图象不经过第三象限,求k的取值范围;
(3)若原方程的一个根大于3,另一个根小于3,求k的最大整数值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某海滨浴场有100个遮阳伞,每个每天收费10元时,可全部租出,若每个每天提高2元,则减少10个伞租出,若每个每天收费再提高2元,则再减少10个伞租出,…,为了投资少而获利大,每个每天应提高( )
A.4元或6元
B.4元
C.6元
D.8元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】竖直上抛的小球离地高度是它运动时间的二次函数,小军相隔1秒依次竖直向上抛出两个小球,假设两个小球离手时离地高度相同,在各自抛出后1.1秒时到达相同的最大离地高度,第一个小球抛出后t秒时在空中与第二个小球的离地高度相同,则t= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读并解答问题:
明朝数学家程大位在其数学著作《直指算法统宗》中以《西江月》词牌叙述了一道“荡秋千”问题:原文:平地秋千未起,踏板一尺离地.送行二步与人齐,五尺人高曾记.仕女佳人争蹴,终朝笑语欢嬉.良工高士素好奇,算出索长有几?译文:如图,有一架秋千,当它静止时,踏板离地![]() 尺,将它往前推送
尺,将它往前推送![]() 尺(水平距离)时,秋千的踏板就和人一样高,这个人的身高为
尺(水平距离)时,秋千的踏板就和人一样高,这个人的身高为![]() 尺,秋千的绳索始终拉得很直,试问绳索有多长?(注:古代
尺,秋千的绳索始终拉得很直,试问绳索有多长?(注:古代![]() 尺为
尺为![]() 步)
步)

建立数学模型:如图,秋千绳索![]() 静止的时候,踏板离地高
静止的时候,踏板离地高![]() 尺(
尺(![]() 尺),将它往前推进两步(
尺),将它往前推进两步(![]() 尺),此时踏板升高离地
尺),此时踏板升高离地![]() 尺(
尺(![]() 尺).已知
尺).已知![]() 于点
于点![]() 于点
于点![]() 于点
于点![]() ,点
,点![]() 在
在![]() 上,
上,![]() ,求秋千绳索(
,求秋千绳索(![]() 或
或![]() )的长度.请解答下列问题:
)的长度.请解答下列问题:
(1)直接写出四边形![]() 是哪种特殊的四边形;
是哪种特殊的四边形;
(2)求![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com