
【题目】已知关于x的一元二次方程x2+(k﹣5)x+1﹣k=0,其中k为常数.
(1)求证:无论k为何值,方程总有两个不相等实数根;
(2)已知函数y=x2+(k﹣5)x+1﹣k的图象不经过第三象限,求k的取值范围;
(3)若原方程的一个根大于3,另一个根小于3,求k的最大整数值.
【答案】
(1)证明:∵△=(k﹣5)2﹣4(1﹣k)=k2﹣6k+21=(k﹣3)2+12>0,
∴无论k为何值,方程总有两个不相等实数根
(2)解:∵二次函数y=x2+(k﹣5)x+1﹣k的图象不经过第三象限,
∵二次项系数a=1,
∴抛物线开口方向向上,
∵△=(k﹣3)2+12>0,
∴抛物线与x轴有两个交点,
设抛物线与x轴的交点的横坐标分别为x1 , x2 ,
∴x1+x2=5﹣k>0,x1x2=1﹣k≥0,
解得k≤1,
即k的取值范围是k≤1
(3)解:设方程的两个根分别是x1 , x2 ,
根据题意,得(x1﹣3)(x2﹣3)<0,
即x1x2﹣3(x1+x2)+9<0,
又x1+x2=5﹣k,x1x2=1﹣k,
代入得,1﹣k﹣3(5﹣k)+9<0,
解得k< ![]() .
.
则k的最大整数值为2
【解析】 (1)先计算b2-4ac,再将b2-4ac的值转化为一个的代数式的平方加上一个正数,即可证出结论。
(2)根据此抛物线的图像不经过第三象限,而抛物线与x轴必有两个交点,可知抛物线的顶点在x轴的下方(第四象限)且图像经过第一、二、四象限,根据二次项的系数可知抛物线开口向上,设抛物线与x轴的交点的横坐标分别为x1 , x2 , 根据x1+x2>0,x1x2≥0,建立关于k的不等式组,求解即可。
(3)设方程的两个根分别是x1 , x2 , 根据已知原方程的一个根大于3,另一个根小于3,建立不等式(x1﹣3)(x2﹣3)<0,,再将不等式转化为含有x1x2和x1+x2的式子,再利用根与系数的关系,建立关于k的不等式,求解即可。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,过点A作AD⊥BC,垂足为D,E为AB上一点,过点E作EF⊥BC,垂足为F,过点D作DG∥AB交AC于点G.
(1)依题意补全图形;
(2)请你判断∠BEF与∠ADG的数量关系,并加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为适应日益激烈的市场竞争要求,某工厂从2016年1月且开始限产,并对生产线进行为期5个月的升降改造,改造期间的月利润与时间成反比例;到5月底开始恢复全面生产后,工厂每月的利润都比前一个月增加10万元.设2016年1月为第1个月,第x个月的利润为y万元,其图象如图所示,试解决下列问题: 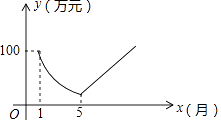
(1)分别求该工厂对生产线进行升级改造前后,y与x之间的函数关系式;
(2)到第几个月时,该工厂月利润才能再次达到100万元?
(3)当月利润少于50万元时,为该工厂的资金紧张期,问该工厂资金紧张期共有几个月?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,BD⊥AC于点D.
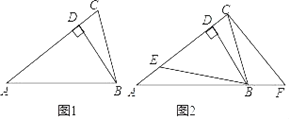
(1)若∠C=∠ABC=2∠A,则∠DBC= °;
(2)若∠A=2∠CBD,求证:∠ACB=∠ABC;
(3)如图2,在(2)的条件下,E是AD上一点,F是AB延长线上一点,连接BE、CF,使∠BEC=∠CFB,∠BCF=2∠ABE,求∠EBC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣x2+2x+k+2与x轴的公共点有两个.
(1)求k的取值范围;
(2)当k=1时,求抛物线与x轴的公共点A和B的坐标及顶点C的坐标;
(3)观察图象,当x取何值时y>0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商人将单价为8元的商品按每件10元出售,每天可销售100件,已知这种商品每提高2元,其销量就要减少10件,为了使每天所赚利润最多,该商人应将销售价(为偶数)提高( )
A.8元或10元
B.12元
C.8元
D.10元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是高,AE是角平分线.
(1)若∠B=30°,∠C=70°,则∠CAE=______°,∠DAE=______°.
(2>若∠B=40°,∠C=80°.则∠DAE=______°.
(3)通过探究,小明发现将(2)中的条件“∠B=40°,∠C=80°”改为“∠C-∠B=40°”,也求出了∠DAE的度数,请你写出小明的求解过程.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“友谊商场”某种商品平均每天可销售100件,每件盈利20元.“五一”期间,商场决定采取适当的降价措施.经调查发现,每件该商品每降价1元,商场平均每天可多售出10件.设每件商品降价x元,请回答:
(1)降价后每件商品盈利元,商场日销售量件(用含x的代数式表示);
(2)求每件商品降价多少元时,商场日盈利可达到最大?最大日盈利是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com