
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 内一点,且
内一点,且![]() ,
,![]() ,
,![]() ,则
,则![]() 等于( )
等于( )
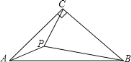
A. 105° B. 120° C. 135° D. 150°
【答案】C
【解析】
把△APC绕点C逆时针旋转90°得到△BDC,根据旋转的性质可得△PCD是等腰直角三角形,BD=AP,∠APC=∠BDC,根据等腰直角三角形的性质求出PD,∠PDC=45°,然后利用勾股定理逆定理判断出△PBD是直角三角形,∠PDB=90°,再求出∠BDC即可得解.
如图,
把△APC绕点C逆时针旋转90°得到△BDC,由旋转的性质得,△PCD是等腰直角三角形,BD=AP=1,∠APC=∠BDC,所以PD=![]() PC=2
PC=2![]() ,∠PDC=45°,∵PD2+BD2=(2
,∠PDC=45°,∵PD2+BD2=(2![]() )2+12=9,PB2=32=9,∴PD2+BD2=PB2,∴△PBD是直角三角形,∠PDB=90°,∴∠BDC=90°+45°=135°,∴∠APC=135°,故答案选C.
)2+12=9,PB2=32=9,∴PD2+BD2=PB2,∴△PBD是直角三角形,∠PDB=90°,∴∠BDC=90°+45°=135°,∴∠APC=135°,故答案选C.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】(1)操作:如图,在已知内角度数的三个三角形中,请用直尺从某一顶点画一条线段,把原三角形分割成两个等腰三角形,并在图中标注相应的角的度数

(2)拓展,△ABC中,AB=AC,∠A=45°,请把△ABC分割成三个等腰三角形,并在图中标注相应的角的度数.

(3)思考在如图所示的三角形中∠A=30°.点P和点Q分别是边AC和BC上的两个动点.分别连接BP和PQ把△ABC分割成三个三角形.△ABP,△BPQ,△PQC若分割成的这三个三角形都是等腰三角形,求∠C的度数所有可能值直接写出答案即可.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,直线![]() 分别交
分别交![]() 轴、
轴、![]() 轴于点
轴于点![]() ,点
,点![]() ,且
,且![]() 、
、![]() 满足
满足![]() .
.
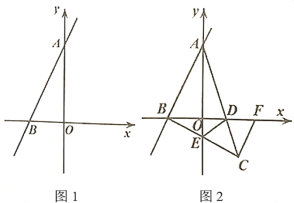
(1)求![]() ,
,![]() 的值;
的值;
(2)以![]() 为边作
为边作![]() ,点
,点![]() 在直线
在直线![]() 的右侧且
的右侧且![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)若(2)的点![]() 在第四象限(如图2),
在第四象限(如图2),![]() 与
与![]() 交于点
交于点![]() ,
,![]() 与
与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() 交
交![]() 轴于点
轴于点![]() .
.
①求证![]() ;
;
②直接写出点![]() 到
到![]() 的距离.
的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是边长为6的等边三角形,
是边长为6的等边三角形,![]() 是
是![]() 边上一动点,由
边上一动点,由![]() 向
向![]() 运动(与
运动(与![]() 、
、![]() 不重合),
不重合),![]() 是
是![]() 延长线上一动点,与点
延长线上一动点,与点![]() 同时以相同的速度由
同时以相同的速度由![]() 向
向![]() 延长线方向运动(
延长线方向运动(![]() 不与
不与![]() 重合),过
重合),过![]() 作
作![]() 于
于![]() ,连接
,连接![]() 交
交![]() 于
于![]() .
.

(1)当![]() 时,求
时,求![]() 的长;
的长;
(2)在运动过程中线段![]() 的长是否发生变化?如果不变,求出线段
的长是否发生变化?如果不变,求出线段![]() 的长;如果发生改变,请说明理由.
的长;如果发生改变,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB⊥y轴,垂足为B,∠BAO=30°,将△ABO绕点A逆时针旋转到△AB1O1的位置,使点B的对应点B1落在直线y=-![]()
![]() x上,再将△AB1O1绕点B1逆时针旋转到△A1B1O2的位置,使点O1的对应点O2落在直线y=-
x上,再将△AB1O1绕点B1逆时针旋转到△A1B1O2的位置,使点O1的对应点O2落在直线y=-![]() x上,依次进行下去…若点B的坐标是(0,1),则点O2020的纵坐标为__________;
x上,依次进行下去…若点B的坐标是(0,1),则点O2020的纵坐标为__________;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),已知![]() ,
,![]() 为
为![]() 的角平分线上一点,连接
的角平分线上一点,连接![]() ,
,![]() ;如图(2),已知
;如图(2),已知![]() ,
,![]() ,
,![]() 为
为![]() 的角平分线上两点,连接
的角平分线上两点,连接![]() ,
,![]() ,
,![]() ,
,![]() ;如图(3),已知
;如图(3),已知![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的角平分线上三点,连接
的角平分线上三点,连接![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ;……,依此规律,第6个图形中有全等三角形的对数是( )
;……,依此规律,第6个图形中有全等三角形的对数是( )

A.21B.11C.6D.42
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于点G,下列结论:①![]() ;②AG=
;②AG=![]() GC;③BE+DF=EF;④
GC;③BE+DF=EF;④![]() .其中正确的是( )
.其中正确的是( )

A.①②③B.①③④C.①②④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC和△DEF为等腰三角形,AB=AC,DE=DF,∠BAC=∠EDF,点E在AB上,点F在射线AC上.
(1)如图1,若∠BAC=60°,点F与点C重合,
①求证:AF=AE+AD.
②求证:AD∥BC.
(2)如图2,若AD=AB,那么线段AF,AE,BC之间存在怎样的数量关系.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com