
【题目】已知△ABC和△DEF为等腰三角形,AB=AC,DE=DF,∠BAC=∠EDF,点E在AB上,点F在射线AC上.
(1)如图1,若∠BAC=60°,点F与点C重合,
①求证:AF=AE+AD.
②求证:AD∥BC.
(2)如图2,若AD=AB,那么线段AF,AE,BC之间存在怎样的数量关系.

【答案】(1)①证明见解析;②证明见解析;(2)AF=AE+BC.
【解析】
(1)①由“SAS”可证△BCE≌△ACD,可得AD=BE,可得结论;
②由全等三角形的性质可得∠DAC=∠EBC=60°,由平行线的判定可得结论;
(2)如图2,在 FA 上截取 FM=AE,连接 DM,由“SAS”可证△AED≌△MFD,可得DA=DM=AB=AC,∠ADE=∠MDF,可证∠ADM=∠BAC,由“SAS”可证△ABC≌△DAM,可得AM=BC,可得结论.
证明:(1)①∵∠BAC=∠EDF=60°,AB=AC,DE=DF,
∴△ABC,△DEF 为等边三角形,
∴BC=AC,CE=CD,∠BCE+∠ACE=∠DCA+∠ECA=60°,
∴∠BCE=∠ACD,
在△BCE 和△ACD 中,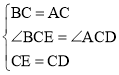 ,
,
∴△BCE≌△ACD(SAS),
∴AD=BE,
∴AE+AD=AE+BE=AB=AF,
即AF=AE+AD;
②∵△BCE≌△ACD,
∴∠DAC=∠EBC,
∵△ABC为等边三角形,
∴∠EBC=∠EAC=∠DAC=60°,
∴∠EBC+∠DAE=∠EBC+∠EAC+∠DAC=180°,
∴AD∥BC.
(2)如图2,在FA上截取FM=AE,连接DM,
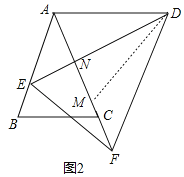
∵∠BAC=∠EDF,∠ANE=∠DNF,
∴∠AED=∠MFD,
在△AED 和△MFD中,
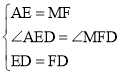 ,
,
∴△AED≌△MFD(SAS),
∴DA=DM=AB=AC,∠ADE=∠MDF,
∴∠ADE+∠EDM=∠MDF+∠EDM,
即∠ADM=∠EDF,
∴∠ADM=∠BAC,
在△ABC 和△DAM 中,
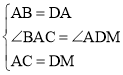
∴△ABC≌△DAM(SAS),
∴AM=BC,
∴AE+BC=FM+AM=AF.
即AF=AE+BC.


科目:初中数学 来源: 题型:
【题目】如图1,在![]() 和
和![]() 中,
中, ![]() ,
,![]() ,
,![]() .
.

(1)若![]() 三点在同一直线上,连接
三点在同一直线上,连接![]() 交
交![]() 于点
于点![]() ,求证:
,求证: ![]() .
.
(2)在第(1)问的条件下,求证: ![]() ;
;
(3)将![]() 绕点
绕点![]() 顺时针旋转得到图2,那么第(2)问中的结论是否依然成立?若成立,请证明你的结论:若不成立,请说明理由.
顺时针旋转得到图2,那么第(2)问中的结论是否依然成立?若成立,请证明你的结论:若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“端午”节前,第一次爸爸去超市购买了大小、质量都相同的火腿粽子和豆沙粽子若干,放入不透明的盒中,此时随机取出火腿粽子的概率为![]() ;妈妈发现小亮喜欢吃的火腿粽子偏少,第二次妈妈又去买了同样的
;妈妈发现小亮喜欢吃的火腿粽子偏少,第二次妈妈又去买了同样的![]() 只火腿粽子和
只火腿粽子和![]() 只豆沙粽子放入同一盒中,这时随机取出火腿粽子的概率为
只豆沙粽子放入同一盒中,这时随机取出火腿粽子的概率为![]() .
.
![]() 请计算出第一次爸爸买的火腿粽子和豆沙粽子各有多少只?
请计算出第一次爸爸买的火腿粽子和豆沙粽子各有多少只?
![]() 若妈妈从盒中取出火腿粽子
若妈妈从盒中取出火腿粽子![]() 只、豆沙粽子
只、豆沙粽子![]() 只送爷爷和奶奶后,再让小亮从盒中不放回地任取
只送爷爷和奶奶后,再让小亮从盒中不放回地任取![]() 只,问恰有火腿粽子、豆沙粽子各
只,问恰有火腿粽子、豆沙粽子各![]() 只的概率是多少?(用字母和数字表示豆沙粽子和火腿粽子,用列清法计算)
只的概率是多少?(用字母和数字表示豆沙粽子和火腿粽子,用列清法计算)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是菱形ABCD边上的一动点,它从点A出发沿在A→B→C→D路径匀速运动到点D,设△PAD的面积为y,P点的运动时间为x,则y关于x的函数图象大致为( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 网格中,每个小正方形的边长都为1,画图请加粗加黑.
网格中,每个小正方形的边长都为1,画图请加粗加黑.
(1)图中格点![]() 的面积为______.
的面积为______.
(2)在图中建立适当的平面直角坐标系,使点![]() ,
,![]() .
.
(3)画出![]() 关于
关于![]() 轴对称的图形
轴对称的图形![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知y是x 的函数,自变量x的取值范围是x >0,下表是y与x 的几组对应值.
x | ··· | 1 | 2 | 3 | 5 | 7 | 9 | ··· |
y | ··· | 1.98 | 3.95 | 2.63 | 1.58 | 1.13 | 0.88 | ··· |
小腾根据学习一次函数的经验,利用上述表格所反映出的y与x之间的变化规律,对该函数的图象与性质进行了探究.
下面是小腾的探究过程,请补充完整:
(1)如图,在平面直角坐标系![]() 中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;

(2)根据画出的函数图象,写出:
①x=4对应的函数值y约为________;
②该函数的一条性质:__________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() (
(![]() ,
,![]() 、
、![]() 、
、![]() 为常数)的图象如图所示,下列
为常数)的图象如图所示,下列![]() 个结论:①
个结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() 为常数,且
为常数,且![]() .其中正确的结论有( )
.其中正确的结论有( )
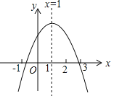
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 、点
、点![]() ,以线段
,以线段![]() 为直角边在第一象限内作等腰直角三角形
为直角边在第一象限内作等腰直角三角形![]() ,
,![]() ,点
,点![]() 为坐标系中的一个动点.
为坐标系中的一个动点.

(1)请直接写出直线![]() 的表达式;
的表达式;
(2)求出![]() 的面积;
的面积;
(3)当![]() 与
与![]() 面积相等时,求实数
面积相等时,求实数![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com