【题目】如图，AB⊥y轴，垂足为B，∠BAO＝30°，将△ABO绕点A逆时针旋转到△AB1O1的位置，使点B的对应点B1落在直线y＝－
x上，再将△AB1O1绕点B1逆时针旋转到△A1B1O2的位置，使点O1的对应点O2落在直线y＝－x上，依次进行下去…若点B的坐标是（0，1），则点O2020的纵坐标为__________；
【答案】
【解析】
观察图象可知，O2、 O4、 O6、...O2020在直线y＝－
x上，OO2＝
的周长=（1+
+2），OO4=2（1+ +2），OO6=3（1+ +2），依次类推OO2020
=1010（1+ +2），再根据点O2020的纵坐标是OO2020的一半，由此即可解决问题．
解：观察图象可知，O2、 O4、 O6、...O2020在直线y＝－x上，
∵∠BAO＝30°，AB⊥y轴，点B的坐标是（0，1），
∴OO2＝的周长=（1+ +2），
∴OO4=2（1+ +2），OO6=3（1+ +2），依次类推OO2020=1010（1+ +2），
∵直线y＝－x与x轴负半轴的交角为30°
∴点O2020的纵坐标=
O O2020=
故答案为：
科目：初中数学 来源： 题型：
【题目】如图，将Rt△ABC绕直角顶点C顺时针旋转90°，得到△A1B1C，连接AA1，若∠AA1B1＝15°，则∠B的度数是（ ）
A. 75° B. 60° C. 50° D. 45°
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】有一个安装有进出水管的30升容器，水管单位时间内进出的水量是一定的，设从
某时刻开始的4分钟内只进水不出水，在随后的8分钟内既进水又出水，得到水量y(升)
与时间x(分)之间的函数关系如图所示．根据图象信息给出下列说法：
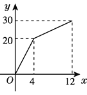
①每分钟进水5升；②当4≤x≤12时，容器中水量在减少；
③若12分钟后只放水，不进水，还要8分钟可以把水放完；
④若从一开始进出水管同时打开需要24分钟可以将容器灌满．
以上说法中正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在一次800米的长跑比赛中，甲、乙两人所跑的路程
（米）与各自所用时间
（秒）之间的函数图像分别为线段
和折线
，则下列说法不正确的是（ ）
A.甲的速度保持不变B.乙的平均速度比甲的平均速度大
C.在起跑后第180秒时，两人不相遇D.在起跑后第50秒时，乙在甲的前面
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】课外兴趣小组活动时，老师提出了如下问题：
如图
，在
中，若
，
，求
边上的中线
的取值范围．
小明在组内经过合作交流，得到了如下的解决方法：延长到
，使得
，再连接
（或将
绕点
逆时针旋转
得到
），把
、
、
集中在
中，利用三角形的三边关系可得
，则
．
[感悟]解题时，条件中若出现“中点”“中线”字样，可以考虑构造以中点为对称中心的中心对称图形，把分散的已知条件和所求证的结论集中到同一个三角形中．
解决问题：受到的启发，请你证明下列命题：如图
，在中，是边上的中点，
，
交于点，
交于点
，连接
．求证：
，若
，探索线段、
、之间的等量关系，并加以证明．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在
中，
，以
为直径的
交
于点
，过点
作
，在
上取一点
，使
，连接
，对于下列结论：①
；②
；③弧
弧
；④为的切线，结论一定正确的是（ ）
A. ②③ B. ②④ C. ①② D. ①③
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图①，△ABC中，AB=AC，点M、N分别是AB、AC上的点，且AM=AN．连接MN、CM、BN，点D、E、F、G分别是BC、MN、BN、CM的中点，连接E、F、D、G．
（l）判断四边形EFDG的形状是 （不必证明）；
（2）现将△AMN绕点A旋转一定的角度，其他条件不变（如图②），四边形EFDG的形状是否发生变化？证明你的结论；
（3）如图②，在（2）的情况下，请将△ABC在原有的条件下添加一个条件，使四边形EFDG是正方形．请写出你添加的条件，并在添加条件的基础上证明四边形EFDG是正方形．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在
网格中，每个小正方形的边长都为1，画图请加粗加黑.
(1)图中格点
的面积为______.
(2)在图中建立适当的平面直角坐标系，使点
，
.
(3)画出关于
轴对称的图形
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
