
����Ŀ����ͼ������ABC�У�AB=AC����M��N�ֱ���AB��AC�ϵĵ㣬��AM=AN������MN��CM��BN����D��E��F��G�ֱ���BC��MN��BN��CM���е㣬����E��F��D��G��
��l���ж��ı���EFDG����״���� ��������֤������
��2���ֽ���AMN�Ƶ�A��תһ���ĽǶȣ������������䣨��ͼ�ڣ����ı���EFDG����״�Ƿ����仯��֤����Ľ��ۣ�
��3����ͼ�ڣ��ڣ�2��������£��뽫��ABC��ԭ�е�����������һ��������ʹ�ı���EFDG�������Σ���д�������ӵ��������������������Ļ�����֤���ı���EFDG�������Σ�

���𰸡���1�����Σ���2�����䣬֤������������3��������������BAC=90�㣬֤��������.
��������
(1) �ı���EFDG��ƽ���ı���, ����Ϊ: ��ͼ1,����AM,��E��F,G��H�ֱ�Ϊ�е�,����������λ�߶����õ�����Ա����, ���ɵ�֤;
(2) ��ͼ��, ����ת�á�BAM=��CAN, ��BAM�ա�CAN��SAS��, BM=CN����E��F�ֱ���MN��BN���е�,�ɵ�EF��DG��EF=DG���ɵ��ı���EFDG��ƽ���ı��Σ��ɵ�FD=![]() BM=EF�������ı���EFDG������;
BM=EF�������ı���EFDG������;
(3) ��BM��CN���ڵ�P��DF��BM���ڵ�Q���ɡ�ABM=��CAN����ABC+��ACB=90��ɵá�BPC=90�㣬��BQD=90�㣬��FDG=90�㣬��������EFDG��������.
�⣺��1���ı���EFDG�����Σ�
�ߵ�D��E��F��G�ֱ���BC��MN��BN��CM���е㣬
��EF�ǡ�NBM����λ�ߣ�DG�ǡ�CBM����λ�ߣ�EG�ǡ�CMN����λ�ߣ�DF�ǡ�BCN����λ�ߣ�
��EF=DG=![]() BM��EG=DF=
BM��EG=DF=![]() CN��
CN��
��AB=AC��AM=AN��
��BM=CN��
��EF=DF=EG=DG��
���ı���EFDG�����Σ�
�ʴ�Ϊ�����Σ�
��2�����䣬
֤��������ת�á�BAM=��CAN��
�ڡ�BAM�͡�CAN�У�
��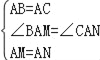 ��
��
���BAM�ա�CAN��SAS����
��BM=CN��
�ߵ�E��F�ֱ���MN��BN���е㣬
��EF��BM��EF=![]() BM��
BM��
ͬ����DG��BM��DG=![]() BM��FD=
BM��FD=![]() CN��
CN��
��EF��DG��EF=DG��
���ı���EFDG��ƽ���ı��Σ�
��EF��CN��BM=CN��
��FD=![]() BM=EF��
BM=EF��
���ı���EFDG�����Σ�
��3��������������BAC=90�㣬
֤������ͼ����BM��CN���ڵ�P��DF��BM���ڵ�Q��
�ɣ�2���á�ABM=��ACN��
�ߡ�BAC=90�㣬
���ABC+��ACB=90�㣬
�ࣨ��ABC����ABM��+����ACB+��ACN��=90�㣬����PBC+��PCB=90�㣬
���BPC=90�㣬
��DF��CN��
���BQD=90�㣬
��DG��BM��
���FDG=90�㣬
������EFDG��������


 ��ǰ����ϵ�д�
��ǰ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
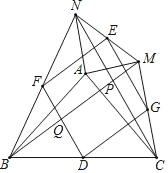
����Ŀ����ͼ����֪��OΪRt��ABCб��AC��һ�㣬�Ե�OΪԲ�ģ�OA��Ϊ�뾶�ġ�O��BC�����ڵ�E����AC�ཻ�ڵ�D������AE�� 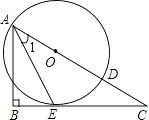
��1����֤��AEƽ�֡�CAB��
��2��̽��ͼ�С�1���C��������ϵ������AE=ECʱtanC��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�O��ֱ����CO��AB�ڵ�O��CD�ǡ�O�����ߣ��е�ΪD������BD����OC�ڵ�E�� 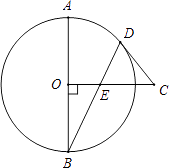
��1����֤����CDE=��CED��
��2����AB=13��BD=12����DE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������һ���ر������������(��ͼ)�������Ϲ����������ĵ���֮������7�������ķ�ͼ�п����۳ɷ��Ϲ�������ӵ���(����)��
![]()
A. 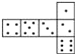 B.
B. 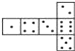 C.
C.  D.
D. 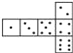
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ֪��a��b��c��d��e���ҡ�1=��2����3=��4����a��cƽ����?Ϊʲô?
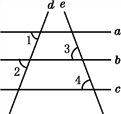
�⣺a��cƽ�У�
���ɣ���Ϊ��1=��2 ��_________________��
����a//b ��__________________________________________��
����3=��4 ��_________________��
����b//c ��__________________________________________��
����a//c ��__________________________________________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�O��ֱ����AC���ң� 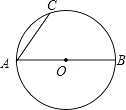
��1�����㰴���沽�軭ͼ����ͼ����������ʱ��ʹ��Ǧ�ʻ�����ȷ�������ʹ�ú�ɫ�ּ���ǩ�ֱ���ڣ��� ��һ��������A����BAC�Ľ�ƽ���ߣ�����O�ڵ�D��
�ڶ���������D��AC�Ĵ��ߣ���AC���ӳ����ڵ�E��
������������BD��
��2����֤��AD2=AEAB��
��3������EO����AD�ڵ�F����5AC=3AB���� ![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������
��1�����㣺��0+2��1�� ![]() ��|��
��|�� ![]() |��
|��
��2��![]() ������x=4��y=��2��
������x=4��y=��2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ����Ϊ2m����Ϊ2n�ij����Σ���ͼ�������ü���������ȷֳ��ĸ�С�����Σ�Ȼ��ͼ�ڵ���״ƴ��һ�������Σ�
(1)����Ϊͼ������Ӱ���ֵ������εı߳�����________��
(2)���������ֲ�ͬ�ķ�����ʾͼ������Ӱ���ֵ����������һ��__________________����������________________��
(3)�۲�ͼ�ڣ�����д������ʽ(m��n)2��(m��n)2��mn֮��Ĺ�ϵ��
(4)Ӧ�ã���֪m��n��11��mn��28(m��n)����m��n��ֵ��
 �١���
�١��� ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��B��C��E������ͬһ��ֱ���ϣ�AC��DE��AC=CE����ACD=��B��
��1����֤��BC=DE
��2������A=40�������BCD�Ķ�����

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com