练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，已知直线a，b，c，d，e，且∠1=∠2，∠3=∠4，则a与c平行吗?为什么?

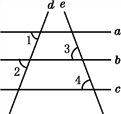
    解：a与c平行；

    理由：因为∠1=∠2 （_________________）

    所以a//b （__________________________________________）

    因为∠3=∠4 （_________________）

    所以b//c （__________________________________________）

    所以a//c （__________________________________________）

    【答案】 已知 同位角相等，两直线平行 已知 同位角相等，两直线平行 平行于同一条直线的两条直线平行

    【解析】因为∠1=∠2（已知）

    所以a//b（同位角相等，两直线平行）

    因为∠3=∠4（已知）

    所以b//c（同位角相等，两直线平行）

    所以a//c（平行于同一条直线的两条直线平行）

    故答案为：已知；同位角相等，两直线平行；已知；同位角相等，两直线平行；平行于同一条直线的两条直线平行

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】（1）在等边三角形ABC中，

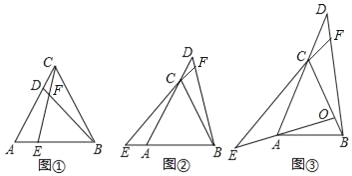
    ①如图①，D，E分别是边AC，AB上的点且AE=CD，BD与EC交于点F，则∠BFE的度数是　 　度；

    ②如图②，D，E分别是边AC，BA延长线上的点且AE=CD，BD与EC的延长线交于点F，此时∠BFE的度数是　 　度；

    （2）如图③，在△ABC中，AC=BC，∠ACB是锐角，点O是AC边的垂直平分线与BC的交点，点D，E分别在AC，OA的延长线上，AE=CD，BD与EC的延长线交于点F，若∠ACB=α，求∠BFE的大小．（用含α的代数式表示）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知数轴上两点A，B对应的数分别为﹣4，8．

    （1）如图1，如果点P和点Q分别从点A，B同时出发，沿数轴负方向运动，点P的运动速度为每秒2个单位，点Q的运动速度为每秒6个单位．

    ①A，B两点之间的距离为　 　．

    ②当P，Q两点相遇时，点P在数轴上对应的数是　 　．

    ③求点P出发多少秒后，与点Q之间相距4个单位长度？

    （3）如图2，如果点P从点A出发沿数轴的正方向以每秒2个单位的速度运动，点Q从点B出发沿数轴的负方向以每秒6个单位的速度运动，点M从数轴原点O出发沿数轴的正方向以每秒1个单位的速度运动，若三个点同时出发，经过多少秒后有MP＝MQ？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】先化简再求值

    （1）3（x2﹣2x﹣1）﹣4（3x﹣2）+2（x﹣1）；其中x＝﹣3

    （2）2a2﹣[（ab﹣4a2）+8ab]﹣ab；其中a＝1，b＝．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知，如图，B，C两点把线段AD分成2：5：3三部分，M为AD的中点，BM=6cm，求CM和AD的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图①，△ABC中，AB=AC，点M、N分别是AB、AC上的点，且AM=AN．连接MN、CM、BN，点D、E、F、G分别是BC、MN、BN、CM的中点，连接E、F、D、G．

    （l）判断四边形EFDG的形状是　 　（不必证明）；

    （2）现将△AMN绕点A旋转一定的角度，其他条件不变（如图②），四边形EFDG的形状是否发生变化？证明你的结论；

    （3）如图②，在（2）的情况下，请将△ABC在原有的条件下添加一个条件，使四边形EFDG是正方形．请写出你添加的条件，并在添加条件的基础上证明四边形EFDG是正方形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】解方程：

    (1)－6x＋2＝2x－14；

    (2)4y－3(20－y)＝6y＋7(y－1)；

    (3)＝1.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读下列解题过程：

    已知a，b，c为△ABC的三边长，且满足a2c2-b2c2=a4-b4，试判断△ABC的形状．

    解：因为a2c2-b2c2=a4-b4， ①

    所以c2(a2-b2)=( a2-b2)( a2+b2). ②

    所以c2= a2+b2． ③

    所以△ABC是直角三角形. ④

    回答下列问题：

    （1）上述解题过程，从哪一步开始出现错误?请写出该步的代码为 ；

    （2）错误的原因为 ；

    （3）请你将正确的解答过程写下来．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，长方形ABCD中，AB=4cm，BC=8cm．点P从点A出发，沿AB匀速运动；点Q从点C出发，沿C→B→A→D→C的路径匀速运动．两点同时出发，在B点处首次相遇后，点P的运动速度每秒提高了3cm，并沿B→C→D→A的路径匀速运动；点Q保持速度不变，继续沿原路径匀速运动，3s后两点在长方形ABCD某一边上的E点处第二次相遇后停止运动．设点P原来的速度为xcm/s.

    （1）点Q的速度为 cm/s（用含x的代数式表示）；

    　（2）求点P原来的速度．

    （3）判断E点的位置并求线段DE的长．

    查看答案和解析>>

    同步练习册答案