【题目】计算
（1）计算：π0+2﹣1﹣ 
﹣|﹣ 
|；
（2）
，其中x=4，y=﹣2．
【答案】
（1）解：原式=1+ 
﹣ ﹣ 
=1﹣
= 
；
（2）解：原式= 
，
当x=4，y=﹣2时，
原式= 
．
【解析】（1）分别根据0指数幂、负整数指数幂及绝对值的性质计算出各数，再根据有理数混合运算的法则进行计算即可；（2）先根据分式混合运算的法则把原式进行化简，再把x=4，y=﹣2代入进行计算即可．
【考点精析】掌握零指数幂法则和整数指数幂的运算性质是解答本题的根本，需要知道零次幂和负整数指数幂的意义： a0=1（a≠0）;a-p=1/ap（a≠0，p为正整数）；aman=am+n(m、n是正整数)；（am）n=amn(m、n是正整数)；(ab)n=anbn(n是正整数)；am/an=am-n(a不等于0，m、n为正整数）；（a/b）n=an/bn(n为正整数)．
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系xOy中，梯形AOBC的边OB在x轴的正半轴上，AC∥OB，BC⊥OB，过点A的双曲线y= 
的一支在第一象限交梯形对角线OC于点D，交边BC于点E．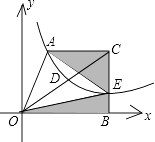
（1）填空：双曲线的另一支在第象限，k的取值范围是；
（2）若点C的坐标为（2，2），当点E在什么位置时，阴影部分的面积S最小？
（3）若 
= 
，S△OAC=2，求双曲线的解析式．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】先化简再求值
（1）3（x2﹣2x﹣1）﹣4（3x﹣2）+2（x﹣1）；其中x＝﹣3
（2）2a2﹣[
（ab﹣4a2）+8ab]﹣ab；其中a＝1，b＝
．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图①，△ABC中，AB=AC，点M、N分别是AB、AC上的点，且AM=AN．连接MN、CM、BN，点D、E、F、G分别是BC、MN、BN、CM的中点，连接E、F、D、G．
（l）判断四边形EFDG的形状是 （不必证明）；
（2）现将△AMN绕点A旋转一定的角度，其他条件不变（如图②），四边形EFDG的形状是否发生变化？证明你的结论；
（3）如图②，在（2）的情况下，请将△ABC在原有的条件下添加一个条件，使四边形EFDG是正方形．请写出你添加的条件，并在添加条件的基础上证明四边形EFDG是正方形．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC为等边三角形，D、E分别是AC、BC上的点，且AD=CE，AE与BD相交于点P，BF⊥AE于点F．若BP=4，则PF的长（ ）
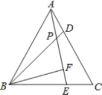
A. 2 B. 3 C. 1 D. 8
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读下列解题过程：
已知a，b，c为△ABC的三边长，且满足a2c2-b2c2=a4-b4，试判断△ABC的形状．
解：因为a2c2-b2c2=a4-b4， ①
所以c2(a2-b2)=( a2-b2)( a2+b2). ②
所以c2= a2+b2． ③
所以△ABC是直角三角形. ④
回答下列问题：
（1）上述解题过程，从哪一步开始出现错误?请写出该步的代码为 ；
（2）错误的原因为 ；
（3）请你将正确的解答过程写下来．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示，在△ABC中，E，G分别是BC，AC上的点，D，F是AB上的点，已知EF⊥AB，垂足为F，CD⊥AB，垂足为D，∠1＝∠2, 试判断∠AGD和∠ACB是否相等，为什么？
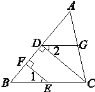
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示，AD是△ABC的角平分线，△ABC的一个外角的平分线AE交边BC的延长线于点E，且∠BAD＝20°，∠E＝30°，则∠B的度数为________．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
