
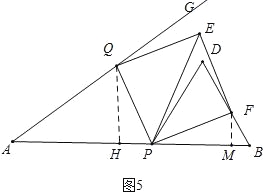
【题目】如图,tan∠GAB=![]() ,AB=10cm,点P从点B出发以5cm/s的速度沿BA向终点A运动,同时点Q以相同的速度从点A出发沿射线AG运动,分别以PB、PQ为边作等边△BPD,正方形PQEF,连接PE,设运动的时间为ts.
,AB=10cm,点P从点B出发以5cm/s的速度沿BA向终点A运动,同时点Q以相同的速度从点A出发沿射线AG运动,分别以PB、PQ为边作等边△BPD,正方形PQEF,连接PE,设运动的时间为ts.
(1)当PE⊥AG时,求t的值;
(2)当△APQ是等腰三角形时,求t的值;
(3)当点F落在△BPD的边上时,请直接写出t的值.

【答案】(1)t=![]() .(2)当△APQ是等腰三角形时,t的值为1s,
.(2)当△APQ是等腰三角形时,t的值为1s,![]() s,
s,![]() s.
s.
(3)t=![]() s或
s或![]() s时,点F落在△BPD的边上.
s时,点F落在△BPD的边上.
【解析】
试题分析:(1)如图1,设PE交AG于点M,过点Q作QN⊥AP于N,在RT△ANQ中,tan∠GAB=![]() ,设QN=3k,AN=4k,则AQ=5k,列出方程即可角问题.
,设QN=3k,AN=4k,则AQ=5k,列出方程即可角问题.
(2)如图2中,过点Q作QH⊥AP于H,分三种情形①当AQ=AP时,②当AP=PQ时,③当AQ=PQ时,列出方程即可.
(3))①如图3中,当点F在直线PD上时,作QH⊥AB于H,②如图4中,当点F在直线PB上时,③如图5中,当点F在BD边上时,作QH⊥AB于H,FM⊥AB于M.
分别列出方程即可解决问题.
试题解析:(1)如图1,设PE交AG于点M.
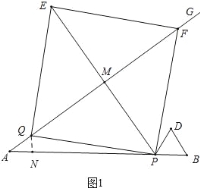
∵四边形PQEF是正方形,∴PE⊥FQ,∴当PE⊥AG时,点F在AG上,∴PM=MQ,
过点Q作QN⊥AP于N,在RT△ANQ中,tan∠GAB=![]() ,设QN=3k,AN=4k,则AQ=5k,
,设QN=3k,AN=4k,则AQ=5k,
∴sin∠MAP=![]() ,cos∠MAP=
,cos∠MAP=![]() ,∵AP=10﹣5t,
,∵AP=10﹣5t,
∴MQ═PM=APsin∠MAP=6﹣3t,AM=APcos∠MAP=8﹣4t,
∵AQ=5t,∴5t+(6﹣3t)=8﹣4t,
∴t=![]() .
.
(2)如图2中,过点Q作QH⊥AP于H,
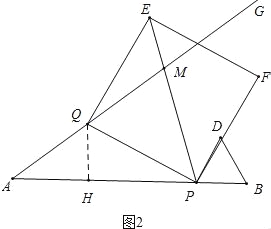
在RT△AQH中,AQ=5t,
∴AH=AQsin∠MAP=5t![]() =4t,QH=AQsin∠MAP=3t,
=4t,QH=AQsin∠MAP=3t,
∵AP=10﹣5t,
∴HP=10﹣9t,
在RT△PQH中,∵∠PHQ=90°,
∴PQ2=HQ2+PH2=(10﹣9t)2+(3t)2=90t2﹣180t+100,
①当AQ=AP时,10﹣5t=5t,解得t=1,
②当AP=PQ时,(10﹣5t)2=90t2﹣180t+100,解得t=![]() (或0舍弃),
(或0舍弃),
③当AQ=PQ时,10﹣5t=3t,解得t=![]() ,
,
综上所述,当△APQ是等腰三角形时,t的值为1s,![]() s,
s,![]() s.
s.
(3)①如图3中,当点F在直线PD上时,作QH⊥AB于H,
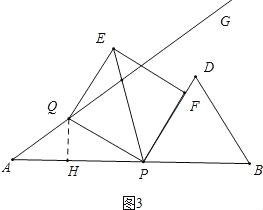
∵∠QOH+∠DPB=90°,∠DPB=60°,
∴∠QPH=30°,
∴PF=PQ=2QH=6t
∴PF>PD,
这种情形不符合题意.
②如图4中,当点F在直线PB上时,
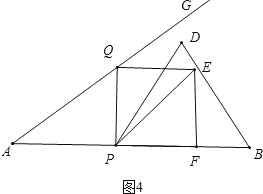
在RT△AQP中,∵AQ=5t.AP=4t,
又∵AP=10﹣5t,
∴4t=10﹣5t,
∴t=![]() ,此时PQ=4t<5t,符合题意.
,此时PQ=4t<5t,符合题意.
③如图5中,当点F在BD边上时,作QH⊥AB于H,FM⊥AB于M.
由△QPH≌△PFM,得到QH=PM=3t,HP=FN=10﹣5t﹣4t=10﹣9t,
在RT△FNB中,∵∠B=60°,
∴BM=![]() FM=
FM=![]() (10﹣9t),
(10﹣9t),
∵PM+BM=PB,
∴3t+![]() (10﹣9t)=5t,
(10﹣9t)=5t,
∴t=![]() .
.
综上所述t=![]() s或
s或![]() s时,点F落在△BPD的边上.
s时,点F落在△BPD的边上.


科目:初中数学 来源: 题型:
【题目】下列说法中正确的是( )
A.位似图形可以通过平移而相互得到
B.位似图形的对应边平行且相等
C.位似图形的位似中心不只有一个
D.位似中心到对应点的距离之比都相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是一张等腰直角三角形彩色纸,将斜边上的高线四等分,然后裁出三张宽度相等的长方形纸条,若恰好可以用这些纸条为一幅正方形美术作品镶边(纸条不重叠),则这张彩色纸的面积与镶嵌所得的作品(如图2)面积之比为( )
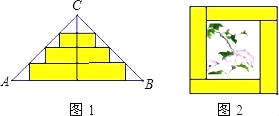
A.2:3 B.3:4 C.1:1 D.4:3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个城镇A、B与两条公路l1、l2位置如图所示,电信部门需在C处修建一座信号发射塔,要求发射塔到两个城镇A、B的距离必须相等,到两条公路l1,l2的距离也必须相等,那么点C应选在何处?请在图中,用尺规作图找出所有符合条件的点C.(不写已知、求作、作法,只保留作图痕迹)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com