
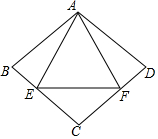
 如图,重叠在一起的菱形硬纸板ABCD和等边三角形硬纸板AEF的边长相等,且等边三角形硬纸板AEF的顶点E,F恰好落在菱形硬纸板的两边上.你能算出∠C的度数吗?
如图,重叠在一起的菱形硬纸板ABCD和等边三角形硬纸板AEF的边长相等,且等边三角形硬纸板AEF的顶点E,F恰好落在菱形硬纸板的两边上.你能算出∠C的度数吗? 分析 连接AC,设∠BAE=y,∠B=x,由△CEF是等边三角形推出∠ECF=60°,又根据对称性得到CA为∠ECF的平分线,因而∠ACE=30°,在△ABC和△BCE中,根据三角形内角和定理列出方程组即可解决问题.
解答 解:连接AC,设∠BAE=y,∠B=x,
∵△CEF是等边三角形,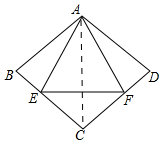
∴∠ECF=60°,又根据对称性得到CA为∠ECF的平分线,
因而∠ACE=30°,
∴在△ABC和△BCE中,根据三角形内角和定理可得方程组
$\left\{\begin{array}{l}{2(30+y)+x=180}\\{2x+y=180}\end{array}\right.$
解得$\left\{\begin{array}{l}{x=80}\\{y=20}\end{array}\right.$,
∴∠B=80°,
∵AB∥CD,
∴∠C=180°-∠B=100°,
点评 本题考查菱形的性质、等边三角形的性质,三角形的内角和定理等知识,解题的关键是学会设未知数,列出方程组解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:选择题
| A. | 过一点有且只有一条直线与已知直线垂直 | |
| B. | 直线外一点与直线上各点连接的所有线段中,垂线最短 | |
| C. | 直线外一点到已知直线的垂线段叫做这点到已知直线的距离 | |
| D. | 平行于同一直线的两条直线平行 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3 | B. | -3 | C. | $\frac{1}{3}$ | D. | $-\frac{1}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
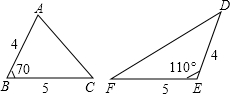 如图,王明同学画了两个不同形状的三角形,并将有关数据在图
如图,王明同学画了两个不同形状的三角形,并将有关数据在图| A. | S△ABC>S△DEF | B. | S△ABC<S△DEF | ||
| C. | S△ABC=S△DEF | D. | 无法确定面积关系 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com