
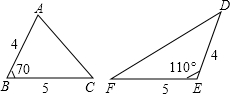
 如图,王明同学画了两个不同形状的三角形,并将有关数据在图
如图,王明同学画了两个不同形状的三角形,并将有关数据在图| A. | S△ABC>S△DEF | B. | S△ABC<S△DEF | ||
| C. | S△ABC=S△DEF | D. | 无法确定面积关系 |
分析 根据题意先分别作△ABC的高AG和△DEF的高DH,根据∠FED=110°,得出∠DEH=70°,再根据已知条件得出AG=DH,最后根据三角形的面积公式得出S△ABC=$\frac{5}{2}$AG和S△DEF=$\frac{5}{2}$DH,从而得出S△ABC=S△DEF.
解答 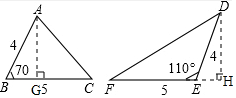 解:作△ABC的高AG,交BC于点G,作△DEF的高DH,交FE的延长线于点H,
解:作△ABC的高AG,交BC于点G,作△DEF的高DH,交FE的延长线于点H,
∵∠FED=110°,
∴∠DEH=70°,
∵∠ABC=70,AB=4,DE=4,
∴AG=DH,
∵BC=5,EF=5,
∴S△ABC=$\frac{1}{2}$BC•AG=$\frac{5}{2}$AG,
S△DEF=$\frac{1}{2}$EF•DH=$\frac{5}{2}$DH,
∵$\frac{5}{2}$AG=$\frac{5}{2}$DH,
∴S△ABC=S△DEF;
故选C.
点评 此题考查了解直角三角形,用到的知识点是三角形的面积公式,关键是根据题意作出两个三角形的高,得出AG=DH.


科目:初中数学 来源: 题型:选择题
| A. | 一个不透明的袋中装有3个红球,5个白球,任意摸出一个球是红球的概率是$\frac{3}{5}$ | |
| B. | 一次摸奖活动的中奖率是l%,那么摸100次奖必然会中一次奖 | |
| C. | 一副扑克牌中,随意抽取一张是红桃K,这是必然事件 | |
| D. | 在367人中至少有两个人的生日相同 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ${({\frac{2}{3}})^2}与\frac{2^2}{3}$ | B. | -22与(-2)2 | C. | -(-5)3与(-5)3 | D. | -(-1)2015与(-1)2016 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
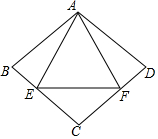 如图,重叠在一起的菱形硬纸板ABCD和等边三角形硬纸板AEF的边长相等,且等边三角形硬纸板AEF的顶点E,F恰好落在菱形硬纸板的两边上.你能算出∠C的度数吗?
如图,重叠在一起的菱形硬纸板ABCD和等边三角形硬纸板AEF的边长相等,且等边三角形硬纸板AEF的顶点E,F恰好落在菱形硬纸板的两边上.你能算出∠C的度数吗?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
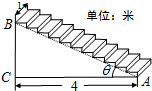 一座楼梯的示意图如图所示,BC是铅垂线,CA是水平线,BA与CA的夹角为θ.现要在楼梯上铺一条地毯,已知CA=4米,楼梯宽度1米,则地毯的面积至少需要( )
一座楼梯的示意图如图所示,BC是铅垂线,CA是水平线,BA与CA的夹角为θ.现要在楼梯上铺一条地毯,已知CA=4米,楼梯宽度1米,则地毯的面积至少需要( )| A. | (4+4sinθ)米2 | B. | $\frac{4}{cosθ}$米2 | C. | (4+$\frac{4}{tanθ}$)米2 | D. | (4+4tanθ)米2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 60 | B. | 70 | C. | 112 | D. | 69 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com