
 小明和同桌小聪在课后复习时,对课本“目标与评定”中一道思考题,进行了认真的探索
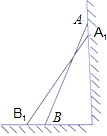
小明和同桌小聪在课后复习时,对课本“目标与评定”中一道思考题,进行了认真的探索分析 (1)在Rt△ABC中,根据已知条件运用勾股定理可将AC的长求出,又知AA1的长可得AC的长,在Rt△A1B1C中再次运用勾股定理可将B1C求出,B1C的长减去BC的长即为底部B外移的距离.
(2)作法与(1)相同;
(3)设梯子顶端从A处下滑x米,点B向外也移动x米,根据勾股定理可得(x+0.7)2+(2.4-x)2=2.52,再解即可.
解答 解:(1)设点B将向外移动x米,即BB1=x,
则B1C=x+0.7,A1C=AC-AA1=$\sqrt{2.{5}^{2}-0.{7}^{2}}$-0.4=2
而A1B1=2.5,在Rt△A1B1C中,由B1C2+A1C2=A1B12得方程(x+0.7)2+22=2.52,
解方程得x1=0.8,x2=-2.2(舍去),
∴点B将向外移动0.8米.
故答案为:(x+0.7)2+22=2.52;0.8,-2.2(舍去),0.8.
(2)①不会是0.9米;
∵AA1=0.9,
∴A1C=2.4-0.9=1.5,
在Rt△A1B1C中,B1C=$\sqrt{2.{5}^{2}-1.{5}^{2}}$=2米,
则BB1=CB1-CB=2-0.7=1.3米.
故梯子底部B外移1.3米.
②有可能.
设梯子顶端从A处下滑x米,点B向外也移动x米,
则有(x+0.7)2+(2.4-x)2=2.52,
解得:x1=1.7或x2=0(舍).
故当梯子顶端从A处下滑1.7米时,点B向外也移动1.7米,即梯子顶端从A处沿墙AC下滑的距离与点B向外移动的距离有可能相等.
点评 本题主要考查了勾股定理的应用及一元二次方程的应用,根据题意得出关于x的一元二次方程是解答此题的关键.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
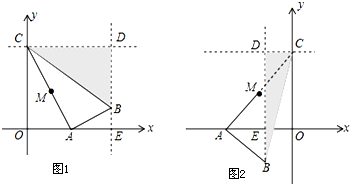
 如图,四边形ABCD是正方形,点G是BC边上任意一点,DE⊥AG,垂足为E,BF⊥AG,垂足为F.
如图,四边形ABCD是正方形,点G是BC边上任意一点,DE⊥AG,垂足为E,BF⊥AG,垂足为F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
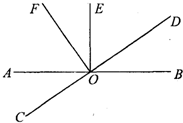 如图,直线AB与CD相交于点D,OE⊥AB,OF⊥CD.
如图,直线AB与CD相交于点D,OE⊥AB,OF⊥CD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知△ABC中,∠A=25°,∠B=40°.
已知△ABC中,∠A=25°,∠B=40°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com