
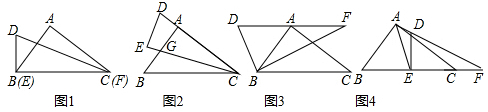
分析 (1)根据三角函数得出AG的长度,再根据三角形的面积公式解答即可;
(2)过A作AG⊥BC于G,BH⊥DF于H,得出AG的长度,再根据三角函数解答即可;
(3)过A作AQ⊥BC于Q,根据相似三角形的性质解答即可.
解答 解(1)BC=EF=10,
∴tan∠DFE=$\frac{3}{10}$,
即$\frac{AG}{AC}=\frac{3}{10}$,
∴AG=$\frac{12}{5}$,S△AGC=$\frac{1}{2}×\frac{12}{5}×8=\frac{48}{5}$,
(2)过A作AG⊥BC于G,BH⊥DF于H,由面积得AG=$\frac{24}{5}$,如图3,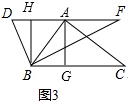
∴BH=$\frac{24}{5}$,
在Rt△FBH中,FH=$\sqrt{1{0}^{2}-(\frac{24}{5})^{2}}=\frac{2\sqrt{481}}{5}$,
∴tanα=$\frac{BH}{FH}=\frac{12\sqrt{481}}{481}$;
(3)过A作AQ⊥BC于Q,如图4: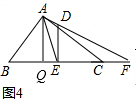
∵△ADE∽△AEF,
∴∠AED=∠F=∠QAE,
∴△AQE∽△FQA,设QE=x,
∴即AQ2=QE•QF,
∴$(\frac{24}{5})^{2}=x(x+10)$,
∴25x2+250x-576=0,
∴${x}_{1}=\frac{-25+\sqrt{1201}}{5}$,${x}_{2}=\frac{-25-\sqrt{1201}}{5}$(舍),
∴$m=BQ+QE=\frac{\sqrt{1201}-7}{5}$,tan∠F=tan∠QAE=$\frac{QE}{AQ}=\frac{-25+\sqrt{1201}}{24}$.
点评 此题考查几何变换问题,关键是根据三角函数得出AG的长度和相似三角形的性质进行分析解答.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小明和同桌小聪在课后复习时,对课本“目标与评定”中一道思考题,进行了认真的探索
小明和同桌小聪在课后复习时,对课本“目标与评定”中一道思考题,进行了认真的探索查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com